The notes of Learning where and what to draw
Overview
Previous method so far only used conditioning variable such as a class label or non-localized caption, and didn’t allow for controlling the location information of objects.
This model learns to perform content controllable and location controllable image synthesis, that is what and where. There are two ways to encode spatial constraints, one is incorporating spatial masking and cropping modules into a text-conditional GAN with spatial transformers, another is locating part of the object by a set of normalized coordinates (x, y) with multiplicative gating mechanism.
Previous work
Two types of transformation from text to image has been proposed, trained to learn one-to-one mappings from the latent space to pixel space, and to learn probabilistic models to approximate the distribution of each pixel TOREAD. Besides, GAN has relatively better sharpness compared to VAE models in general.
Spatial Transformer Networks (STN) is an effective visual attention mechanism
Network structure
GAN and Joint embedding structure used in this model is articulated in the notes of Generative Adversarial Text to Image Synthesis
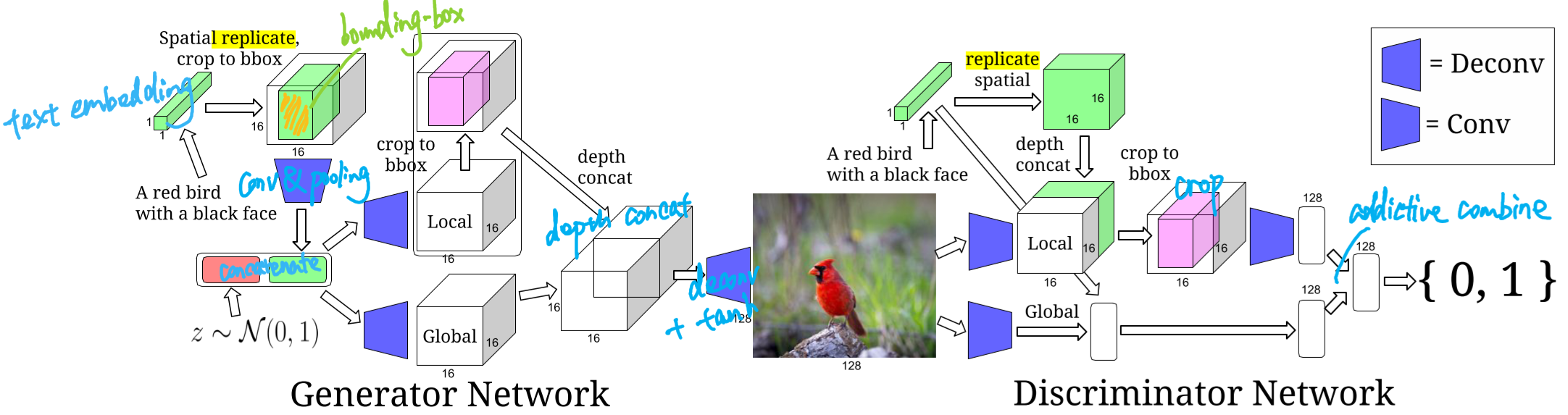
Bounding-box conditional model
Keypoint conditional model
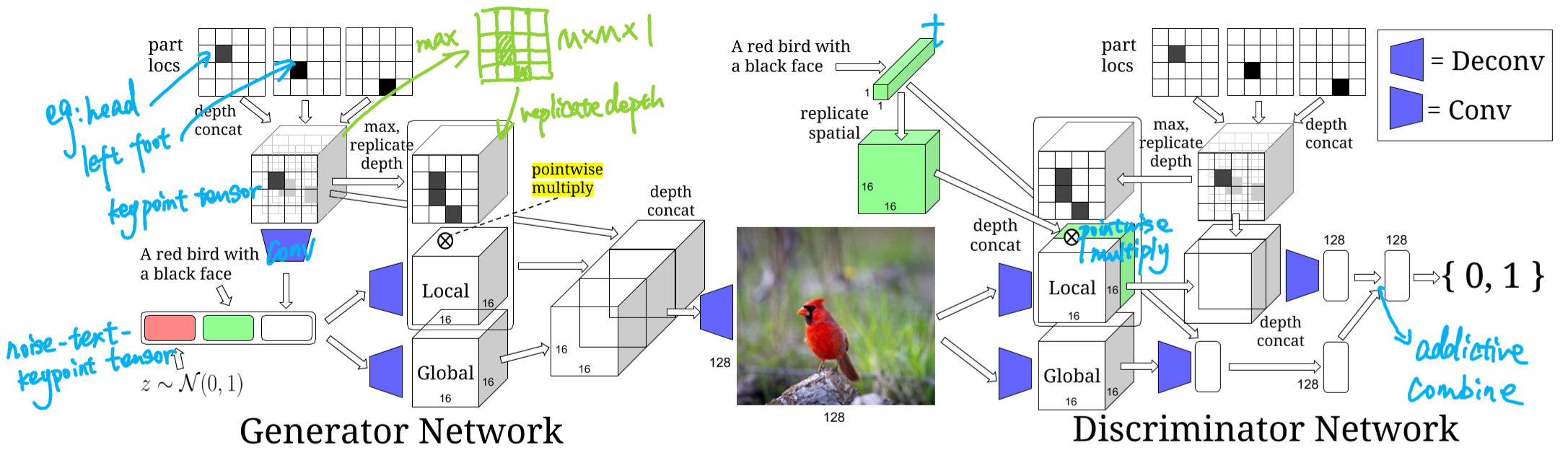
Conditional keypoint generation model
The purpose is to have acceess to all of the conditional distributions of keypoints, given a subset of observed keypoints and the text description. However, a simple autoencoder is sparse and would not suffice.
The keypoint generation GAN is proposed to build datasets with full keypoints using gating mechanism given only a few of visible variable.
The discriminator $D$ of the GAN is simple which only distinguish real keypoints and text $ \left( \mathbf{k}_{real}, \mathbf{t}_{real} \right) $ from synthetic keypoints.
The generator $G$ is relatively complicated and formulated as follows:
\[G_{k}(z, \mathbf{t}, \mathbf{k}, \mathbf{s}) :=\mathbf{s} \odot \mathbf{k}+(1-\mathbf{s}) \odot f(z, \mathbf{t}, \mathbf{k})\]where $k_{i}:=\left\{ x_{i}, y_{i}, v_{i} \right\}$, $i = 1,…,K$ and $x$ and $y$ indicate thee rows and columns position, $v$ is a bit set to 1 if the part is absolutely visible and 0 otherwise. Note that $\mathbf{k} \in[0,1]^{K \times 3}$ encode the keypoints into a matrix. Switch units $\mathbf{s} \in{0,1}^{K}$ is to specified previously by for example user, which set the $i$-th entry of $K$ to 1 if the corresponding $i$-th part is 1 and 0 otherwise. $\odot$ denotes pointwise multiplication and $f$ is a 3-layer fully-connected network to transform concatenated $z$, $t$ and flattened $k$ of shape $\mathbb{R}^{Z+T+3 K}$ to the shape of $\mathbb{R}^{3 K}$
As stated above, parameters of $f$ is trainable. TOREAD
In order for $G_{k}$ to capture all of the conditional distributions over keypoints, during training switch units $s$ is randomly sampled.