The notes of Semi-parametric Image Synthesis
Overview
It presents a semi-parametric approach of photographic image synthesis from semantic layouts.
Preliminaries
- Parametric method
Current parametric method generally refers to using deep networks to represent all data concerning photographic appearance in weights. It has advantages of end-to-end training over highly expressive models.
- Non-parametric method
Non-parametric method in the past draw on the database of image segments which is used to retrieve photographic references provided as source material. It has an ability to draw on large databases of original photographic content at test time.
- Semi-parametric method
This paper combines the complementary strengths of parametric and nonparametric techniques. Given a semantic layout, the system retrieves compatible segments from the database. The retrieved segments are used as raw material for synthesis and then composited onto the canvas. Deep networks help to align the components, resolve occlusion relationships and rectify the canvas to the final photographic image as output.
- Analogy
In summary, it draws an analogy that the practices of human painter who do not draw purely on memory, comparing to the weights of neural networks, but also use external references from around actual world, in contrast to the database of image segmentations, to reproduce the detailed object appearance.
Pipeline
The first and crucial thing is to build the External memory bank (database) $M$. A set of color images and corresponding semantic layouts make a pair to generate $M$ with different semantic categories.
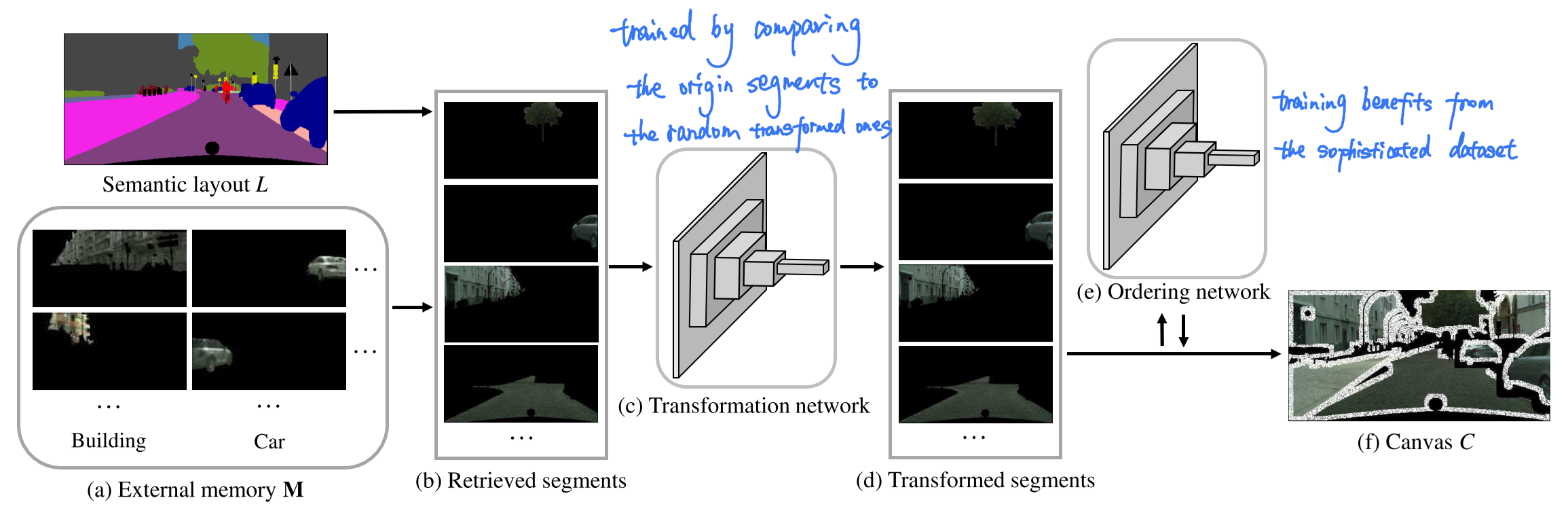
At test time, Semantic map $L \in{0,1}^{h\times w \times c} $, where $h \times w$ is the size of images and $c$ is the number of semantic classes, which was not seen during training, is decomposed into connected components $\left\{L_{i}\right\}$. For each $\left\{L_{i}\right\}$, a compatible segment $P_{i}$ from $M$ is retrieved based on shape, location and context and then aligned to $L_{i}$ by a spatial Transformation network. With the help of the Ordering network, relative front-back order of segments is determined and canvas $C$ is synthesized with deliberately elided boundaries of retrieved segments.
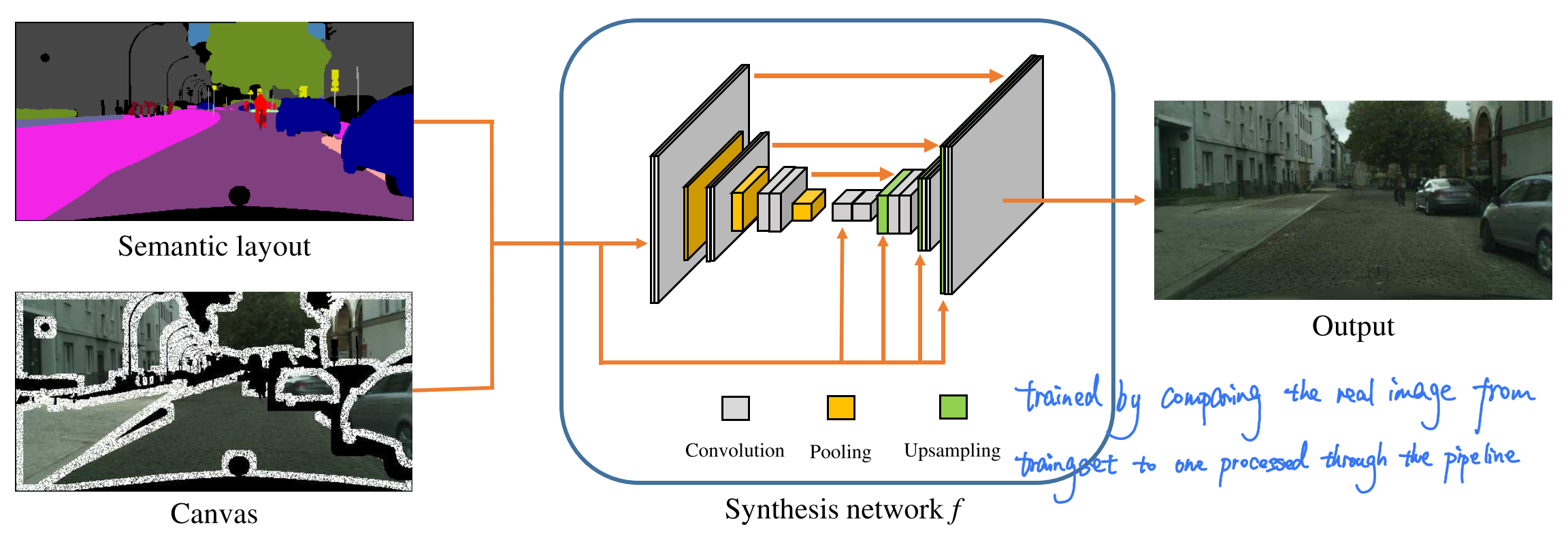
A Synthesis network $f$ uses the canvas $C$ and the input layout $L$ as input, inpainting the missing regions, harmonizing retrieved segments, blending boundaries, synthesizing shadows and otherwise adjusting the final appearance.
Furthermore, cascaded refinement network is used to convert coarse imcomplete layouts to dense pixelwise layouts.
Canvas building
Representation of memory bank
A segment $P_{i}$ is associated with a tuple $\left(P_{i}^{\text {color}}, P_{i}^{\text {mask}}, P_{i}^{\text {cont}}\right)$, where $P_{i}^{c o l o r} \in \mathbb{R}^{h \times w \times 3}$ is a color image that contains the segment (other pixels are zeroed out as showed in the first image), $P_{i}^{m a s k} \in{0,1}^{h \times w \times c}$ is a binary mask that specifies the segment’s footprint, and $P_{i}^{c o n t} \in{0,1}^{h \times w \times c}$ is a semantic map representing the semantic context around $P_{i}$ within a bounding box enlarged by 25% to the $P_{i}^{\text {color}}$.
Segment retrieval
Given a semantic layout $L$ at test time, $L_{j}^{\text {mask}}$ and $L_{j}^{\text {cont}}$ is computed for each semantic segment $L_{j}$, by analogy with the definitions of $P_{i}$. Then the most compatible segment $P_{\sigma(j)}$ is computed over the intersection-over-union score TOREAD $\operatorname{IoU}$ as follows where the first term measures the overlap of the shapes while another measures the similarity of surrounding which helps the retrieve when surrounding affects appearance. $i$ iterates over segments in $M$ that have the same semantic class as $L_{i}$.
\[\sigma(j)=\underset{i}{\arg \max } \operatorname{IoU}\left(P_{i}^{\operatorname{mask}}, L_{j}^{\operatorname{mask}}\right)+\operatorname{IoU}\left(P_{i}^{c o n t}, L_{j}^{c o n t}\right)\]Transformation network
The transformation network $T$ is designed to transform $P_{\sigma(j)}$ to align $L_{j}$ via translation, rotation, scaling and clipping while preserving the integrity of the appearance.
By simulating the inconsistencies in shape, scale and location that $T$ encounters at test time, $T$ can be trained with the input $\hat{P}_{i}^{\text { color }}$ which is applied random affine transformations and cropped from $P_{i}^{\text { color }}$.
The loss function for $T$ is as follows, and is defined over the color images rather than the mask so as to be more specific and better to constran the transformation.
\[\mathcal{L}_{T}\left(\theta^{T}\right)=\sum_{P_{i} \in \mathbf{M}}\left\|P_{i}^{c o l o r}-T\left(P, P_{i}^{m a s k}, \hat{P}_{i}^{c o l o r} ; \theta^{T}\right)\right\|_{1}\]Ordering network
The ordering network is to determine the front-back ordering of adjacent object segments whose output is a $c$-dimensional one-hot vector as multi-classcification problem with absolute cross-entropy loss.
For the training of this network, it is totally take the advantage of datasets like Cityscapes and NYU.
Image synthesis
Encoder-decoder architecture
The synthesis network $f$ has an encoder-decoder structure with skip connections to synthesize the final photo.
-
Encoder constructs a multiscale representation of the input $\left(C, L \right)$ based on VGG-19, and capture long-range correlations that can help the decoder harmonize color, lighting, and texture.
-
Decoder uses this representation to synthesize progressively finer feature maps, culmiating in full-resolution output. It also based on the cascaded refinement network as the framework showed above.
Training
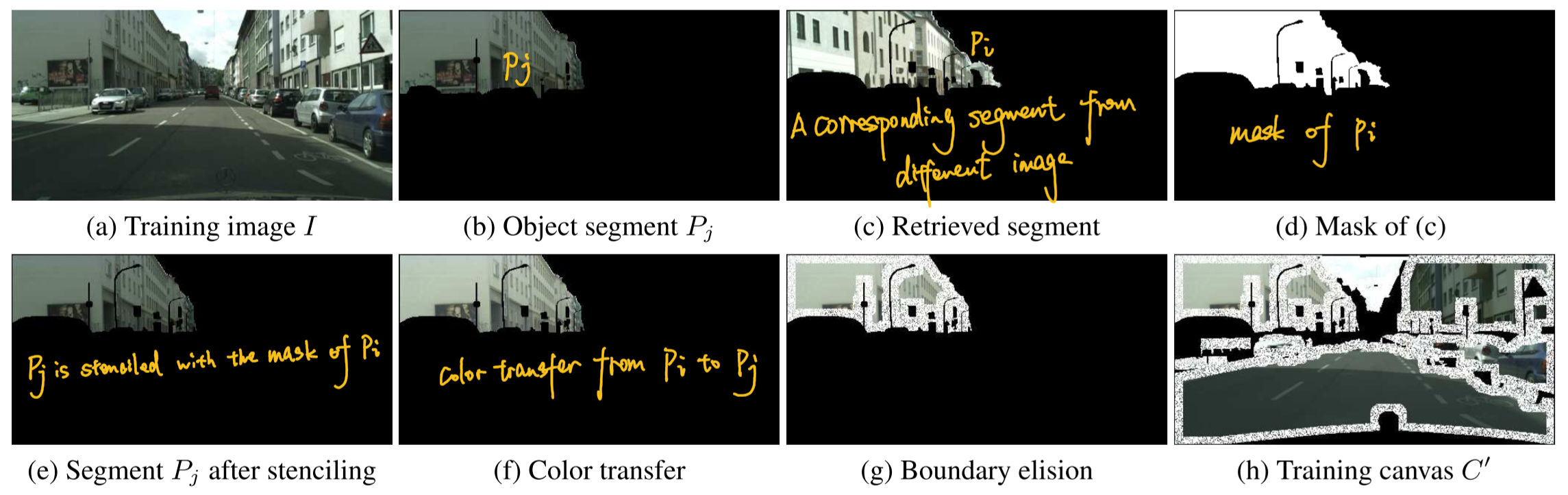
To train the network $f$, artifacts of canvas with poor quality at test time must be simulated. Given a semantic layout $L$ and a corresponding color image $I$ from the training set, stenciling, color transfer and boundary elision to the pair $\left(I, L \right)$ is implemented to synthesize the simulated canvas $C^{\prime}$ . Thus $f$ is trained to take the pair $\left(C^{\prime}, L\right)$ and recover the original image $I$.
\[\mathcal{L}_{f}\left(\theta^{f}\right)=\sum_{(I, L) \in \mathcal{D}} \sum_{l} \lambda_{l}\left\|\Phi_{l}(I)-\Phi_{l}\left(f\left(C^{\prime}, L\right) ; \theta^{f}\right)\right\|_{1}\]where $\Phi_{l}$ is the feature tensor in layer $l$.
-
Stenciling: for each training image $I$ which is masked out the region of retrieved segments from set training, the network $f$ will learn to generate the context and foreground.
-
Color transfer: different segments on the canvas generally have inconsistent tone and illumination since xxxx. Therefore, to modify the color distribution of $P_{j}$ in $C^{\prime}$, segment $P_{i}$ with the same semantic class fom $M$ is retrieved and used as the target of transferring.
-
Boundary elision: segment boundary is masked out randomly so as that the network $f$ is forced to learn to synthesize content near boundaries. Inconsistencies along boundries arise not only inside segments. TOREAD
Conclusion
SIMS approach demonstrate to produce considerably more realistic image than recent purely parametric techniques (entirely depend on weights of neural network without database).
SIMS in a sense lower-bounded by the performance of parametric methods, that if the memory bank is not useful, the network $f$ can simply ignore the canvas and perform parametric synthesis based on the input semantic layout. TOREAD
Future work includes:
-
acceleration of SIMS
-
other forms of input can be used, like semantic instance segmentation or textual descriptions
-
not end-to-end
-
the frontier of video synthesis