The Notes of Computer Graphics Ⅱ

A swift and brutal review of Linear Algebra

Computer Graphics’ Dependencies

• Basic mathematics
  • Linear algebra
  • Calculus
  • Statistics
• Basic physics
  • Optics (Advanced: if we could not suppose the light travels in straight lines but interacts with a surface material in a form of light wave?)
  • Mechanics
• Misc.
  • Signal processing (for anti-alias)
  • Numerical analysis (rendering is to find a solution of calculus defined by recursion, simulation is to solve FEA, Finite Element Analysis, or diffusion equation)
• A bit of aesthetics

Vector

• Direction and length
• Usually written as $\vec{a}$ or using start and end point $\overrightarrow{AB}$
• No absolute starting position

Vector Normalization

• Magnitude (length) of a vector written as $|\vec{a}|$
• Unit vector
  • A vector with length of 1
  • $\hat{a}=\vec{a} /|\vec{a}|$
  • represent directions

Vector Addition

• Geometrically: Parallelogram law & Triangle law
• Algebraically: Simply add coordinates

Dot (scalar) Product

$\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$

For unit vectors:

$\cos \theta=\hat{a} \cdot \hat{b}$

Some properties:

$\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}$

$\vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}$

$(k \vec{a}) \cdot \vec{b}=\vec{a} \cdot(k \vec{b})=k(\vec{a} \cdot \vec{b})$

For component-wise multiplication of vectors in Cartesian coordinates:

$$\vec{a} \cdot \vec{b}=\left(\begin{matrix}x_{a} \\ y_{a} \\ z_{a}\end{matrix}\right) \cdot\left(\begin{matrix}x_{b} \\ y_{b} \\ z_{b}\end{matrix}\right)=x_{a} x_{b}+y_{a} y_{b}+z_{a} z_{b}$$

Four common usages of dot product:

1. To find angle between two vectors

2. To find projection of one vector on another:

   To Calculate $\vec{b}_{\perp}$: projection of $\vec{b}$ onto $\vec{a}$

   • $\vec{b}_{\perp}$ must be along $\vec{a}$, thus $\vec{b}_{\perp}=k \hat{a}$
   • The magnitude of $k$ is $\left|\vec{b}_{\perp}\right|=|\vec{b}| \cos \theta$
3. To measure how close two directions are
4. To decompose a vector: $\vec{b}$, $\vec{b}_{\perp}$, $\vec{b}-\vec{b}_{\perp}$

Cross Product

$|a \times b|=|a||b| \sin \phi$

• Cross product is orthogonal to two initial vectors
• Direction determined by right-hand rule
• To construct coordinate systems

Some properties:

$\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}$

$\vec{a} \times \vec{a}=\overrightarrow{0}$

$\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}$

$\vec{a} \times(k \vec{b})=k(\vec{a} \times \vec{b})$

For cross product in Cartesian Formula:

$$\vec{a} \times \vec{b}=\left(\begin{array}{l}y_{a} z_{b}-y_{b} z_{a} \\ z_{a} x_{b}-x_{a} z_{b} \\ x_{a} y_{b}-y_{a} x_{b}\end{array}\right)$$

Or using matrix form:

$$\vec{a} \times \vec{b}=A^{*} b=\left(\begin{array}{ccc}0 & -z_{a} & y_{a} \\ z_{a} & 0 & -x_{a} \\ -y_{a} & x_{a} & 0\end{array}\right)\left(\begin{array}{l}x_{b} \\ y_{b} \\ z_{b}\end{array}\right)$$

Two common usages of cross product:

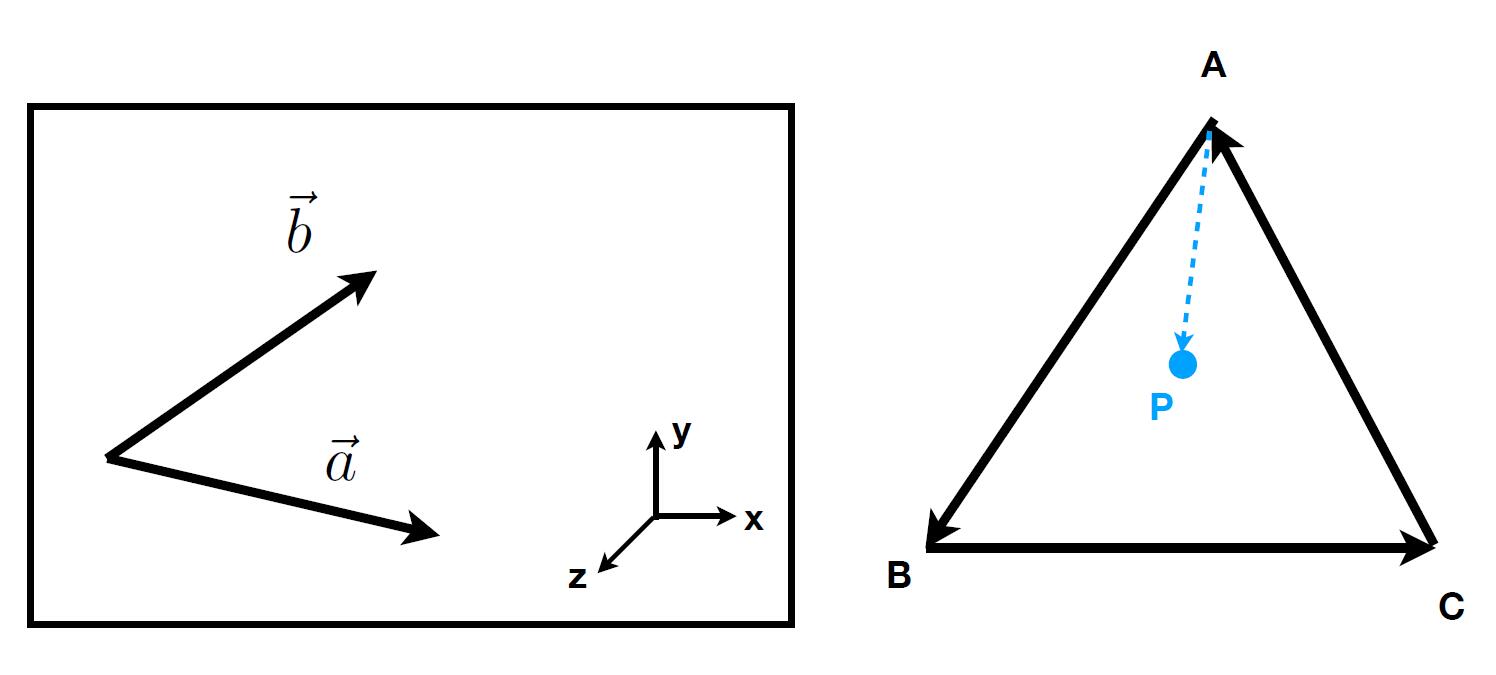
1. To determine left/right: check if the cross product of two vectors points to the outside of the screen or out.
2. To determine inside/outside: check if the cross product of $\overrightarrow{AB} \times \overrightarrow{AP}$ and $\overrightarrow{BP} \times \overrightarrow{BP}$ and $\overrightarrow{CA} \times \overrightarrow{CP}$ all directed to the outside of the screen.

Orthonormal Coordinate

We can decompose any vectors $\vec{p}$ by 3 unit vectors:

$\vec{p}=(\vec{p} \cdot \vec{u}) \vec{u}+(\vec{p} \cdot \vec{v}) \vec{v}+(\vec{p} \cdot \vec{w}) \vec{w}$
, where
$|\vec{u}|=|\vec{v}|=|\vec{w}|=1$
$\vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{w}=\vec{u} \cdot \vec{w}=0$
$\vec{w}=\vec{u} \times \vec{v} \quad$

Matrix

• 2D arrays that haunt in every CS course
• In Graphics, pervasively used to represent transformations

Matrix-Matrix Multiplication

• columns in A must = rows in B
• Element (i, j) in the product is the dot product of row i from A and column j from B

Some properties:

• Non-commutative: ($AB$ and $BA$ are different in general)
• Associative and distributive:
  • $(AB)C = A(BC)$
  • $A(B+C) = AB + AC$

Matrix-Vecotr Multiplication

• Treat vector as a column matrix (Mx1)
• Treat vector as the right multiplier of the matrix (as a point)
• Key for transforming points

Transpose of a Matrix

• Switch rows and columns ($ij$ to $ji$)
• $(A B)^{T}=B^{T} A^{T}$

Identity Matrix and Inverses

$$I_{3 \times 3}=\left(\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right)$$

$A A^{-1}=A^{-1} A=I$

$(A B)^{-1}=B^{-1} A^{-1}$

Reference

• GAMES101, Lingqi Yan