The Notes of Computer Graphics Ⅲ

2D/3D Transformation, Viewing Transformation

Linear Transformations

Scale

\[\left[\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right]=\left[\begin{array}{ll}s_{x} & 0 \\ 0 & s_{y}\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right]\]

Reflection

\[\left[\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right]=\left[\begin{array}{cc}-1 & 0 \\ 0 & 1\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right]\]

Shear

\[\left[\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right]=\left[\begin{array}{ll}1 & a \\ 0 & 1\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right]\]

Rotation

\[\mathbf{R}_{\theta}=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \hat{\theta}\end{array}\right]\]

Tip: For the rotation matrix $M$, which is always normalized in orthogonal form. Thus the transposed matrix $M^{T}$ is exactly inversed matrix $M^{-1}$, that is: $M^{T}=M^{-1}$, where $M$ is orthogonal matrix

Linear Transformations

• Use the same dimension matrix

\[\begin{aligned}\left[\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right] &=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right] \\ \mathbf{x}^{\prime} &=\mathbf{M} \mathbf{x} \end{aligned}\]

Affine Transformations

Homogeneous Coordinate

• Translation cannot be represented in matrix form

\[\left[\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right]=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right]+\left[\begin{array}{l}t_{x} \\ t_{y}\end{array}\right]\]

Hence, translation is Not linear transform

• But we don’t want translation to be a special case, so is there a unified way to represent all transformations?

• Add a third coordinate, and use 3D matrix to represent translations:

  • 2D point $=(x, y, 1)^{\top}$
  • 2D vector $=(x, y, 0)^{\top}$

\[\left(\begin{array}{c}x^{\prime} \\ y^{\prime} \\ w^{\prime}\end{array}\right)=\left(\begin{array}{ccc}1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1\end{array}\right) \cdot\left(\begin{array}{l}x \\ y \\ 1\end{array}\right)=\left(\begin{array}{c}x+t_{x} \\ y+t_{y} \\ 1\end{array}\right)\]

• Valid operation if w-coordinate of result is 1 or 0
  • vector + vector = vector
  • point - point = vector
  • point + vector = point
  • point + point = ?

Info: In homogenous coordinates,
\(\left(\begin{array}{l}x \\ y \\ w\end{array}\right)\) is the 2D point \(\left(\begin{array}{c}x / w \\ y / w \\ 1\end{array}\right), w \neq 0\)
Thus, point + point = midpoint of two points

Affine Transformations

• Affine map = linear map + translation

\[\left(\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right)=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right) \cdot\left(\begin{array}{l}x \\ y\end{array}\right)+\left(\begin{array}{l}t_{x} \\ t_{y}\end{array}\right)\]

• Using homogenous coordinates:

\[\left(\begin{array}{l}x^{\prime} \\ y^{\prime} \\ 1\end{array}\right)=\left(\begin{array}{lll}a & b & t_{x} \\ c & d & t_{y} \\ 0 & 0 & 1\end{array}\right) \cdot\left(\begin{array}{l}x \\ y \\ 1\end{array}\right)\]

Note: This means linear transform first, and then translation.

Inverse Transform

$\mathbf{M}^{-1}$ is the inverse of transform $\mathbf{M}$ in both a matrix and geometric sense.

Composite transform

Composing Transforms

• Matrix multiplication is not commutative
• For a sequence of affine transforms $A_{1}, A_{2}, A_{3}, \ldots$
  • Compose by matrix multiplication to speed up: \(A_{n}\left(\ldots A_{2}\left(A_{1}(\mathbf{x})\right)\right)=\mathbf{A}_{n} \cdots \mathbf{A}_{2} \cdot \mathbf{A}_{1} \cdot\left(\begin{array}{l}x \\ y \\ 1\end{array}\right)\)
  • Pre-multiply n matrices to obtain a single matrix $\mathbf{A}_{n} \cdots \mathbf{A}_{2} \cdot \mathbf{A}_{1}$ representing combined transform

Decomposing Complex Transforms

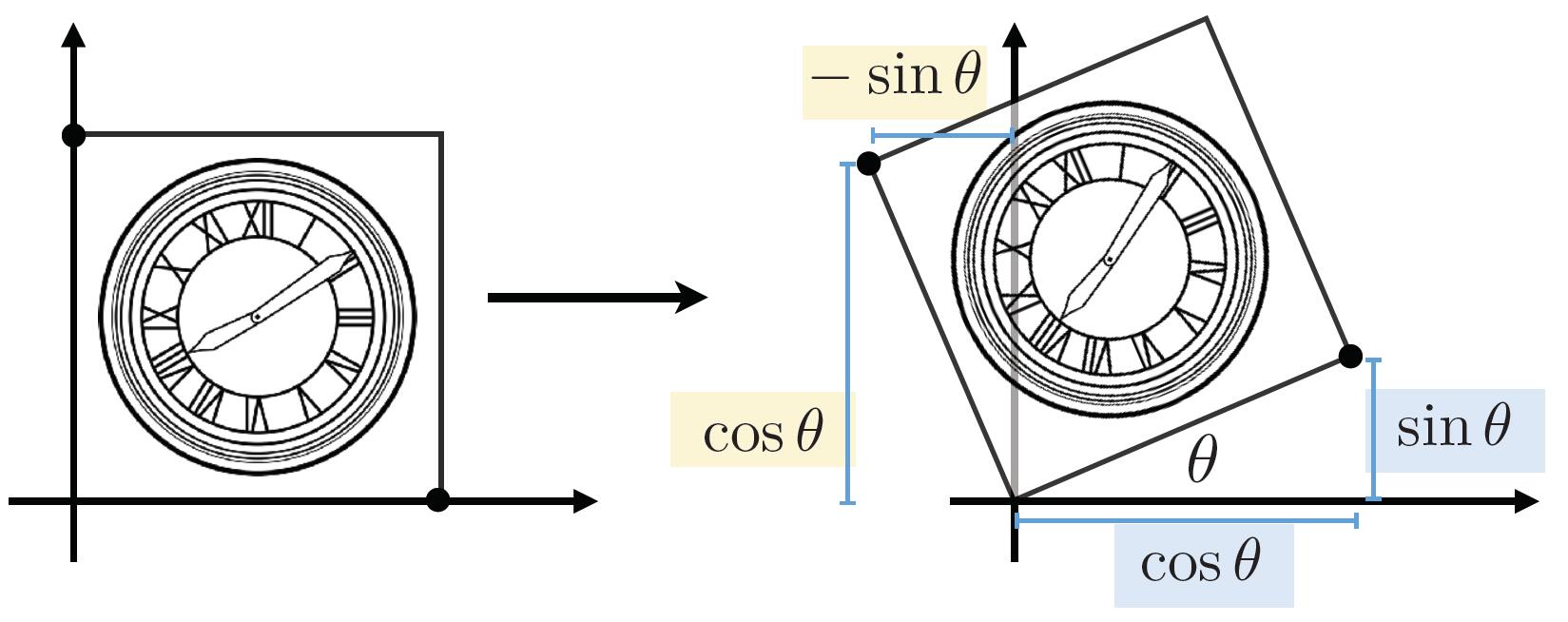
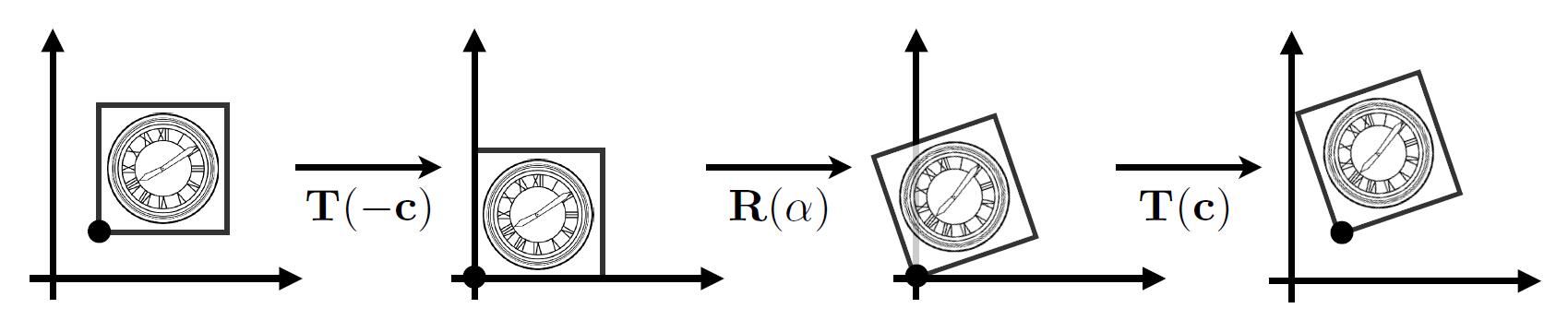
How to rotate around a given point c?

1. Translate center to origin
2. Rotate
3. Translate Back

3D transformations

Rotation around x, y, z-axis

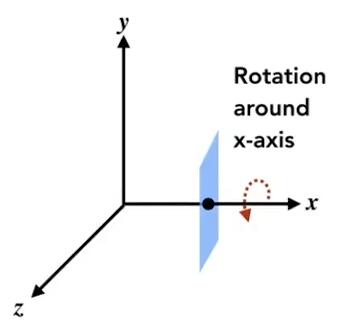
\(\mathbf{R}_{x}(\alpha)=\left(\begin{array}{cccc}1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1\end{array}\right)\)
\(\mathbf{R}_{y}(\alpha)=\left(\begin{array}{cccc}\cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1\end{array}\right)\)
\(\mathbf{R}_{z}(\alpha)=\left(\begin{array}{cccc}\cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right)\)

Caveat: In $\mathbf{R}_{y}$, where we use right-hand rule $z \times x$ get $y$, so the $\alpha$ is opposite.

Euler angles

• To represent any 3D rotation from $\mathbf{R}_{x}, \mathbf{R}_{y}, \mathbf{R}_{z}$,

$\mathbf{R}_{x y z}(\alpha, \beta, \gamma)=\mathbf{R}_{x}(\alpha) \mathbf{R}_{y}(\beta) \mathbf{R}_{z}(\gamma)$

• $(\alpha, \beta, \gamma)$ is Euler angles

• Often used in flight simulator:

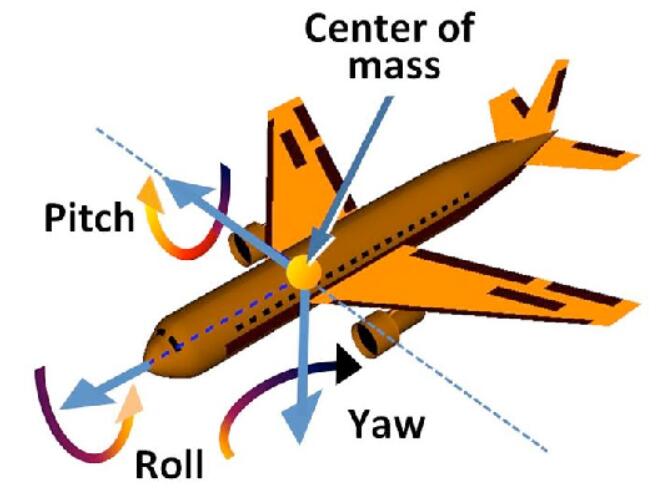
• Eluer angles may cause Gimbal lock: The loss of one degree of freedom.
  • This suitation occurs when the axes of two of the three gimbals are driven into a parallel configuration as the below shows.
  • Use Unit quaternions to solve this problem

Rodrigues’ Rotation Formula

• Rotation by angle $\alpha$ around axis $n$ (axis $n$ goes through the origin)

\[\mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc}0 & -n_{z} & n_{y} \\ n_{z} & 0 & -n_{x} \\ -n_{y} & n_{x} & 0\end{array}\right)}_{\mathbf{N}}\]

• Formula derivation

• If the rotation axis doesn’t go through the origin, but at $p$

  • Translate the axis to origin. $T(-p)$
  • Rotate. $R(n, \alpha)$
  • Translate the axis back: $T(p)$
  • Thus: $T(p)R(n, \alpha)T(-p)$

Viewing transformation

• View / Camera Transformation
• Projection transformation
  • Orthographics projection
  • Perspective projection

A vivid analogy

• Analogous to taking a photo:
  • Find a good place and arrage people (model transformation)
  • Find a good “angle” to put the camera (view transformation)
  • Cheese! (projection transformation)

View / Camera Transformation

Define the camera

• Define the camera first (suppose every objects has been arranged properly)
  • Position $\vec{e}$
  • Look-at / gaze direction $\hat{g}$
  • up direction $\hat{t}$

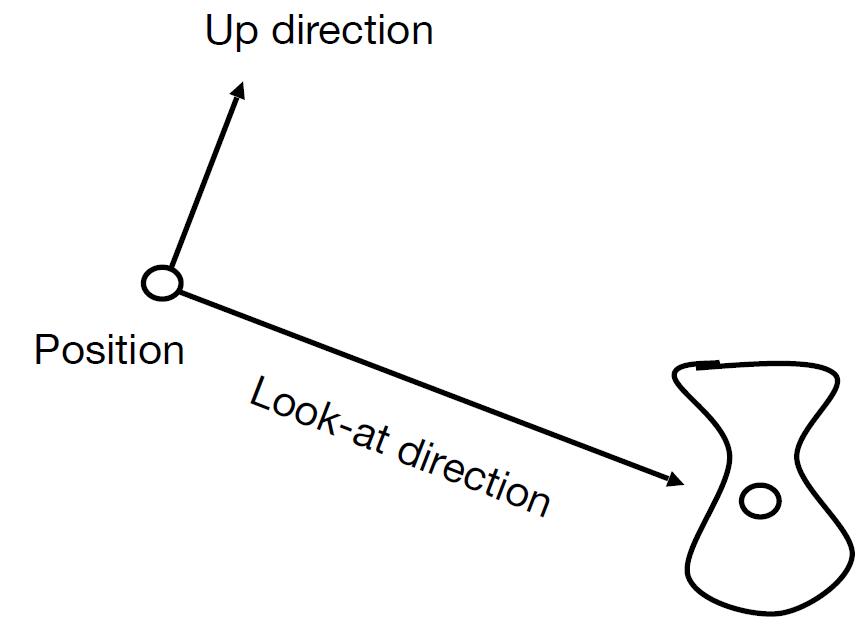
• Key observation: If the camera and all objects move together, the photo will be the same. Thus we transform the camera to the fixed origin point.
  • Position: the origin
  • Look-at direction: -Z
  • up direction: Y
  • Then transform the objects along with the fixed camera

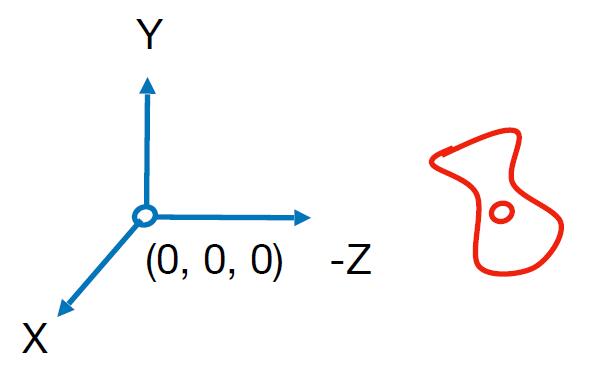
Transform the camera

• Transform the camera by $M_{\text {view}}$
  • To locate it at the origin, up at $Y$, look at $Z$
    • Translates $e$ to origin
    • Rotates $t$ to $Y$
    • Rotates $g$ to $-Z$
    • If $t$ to $Y$ and $g$ to $-Z$, then $\hat{g} \times \hat{t}$ will be to $X$

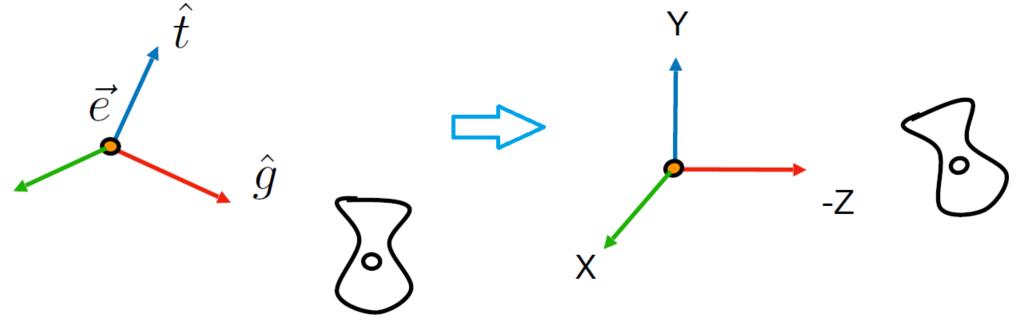
• $M_{\text {view}}=R_{\text {view}}T_{\text {view}}$
  • Translate $e$ to origin
    \(T_{v i e w}=\left[\begin{array}{cccc}1 & 0 & 0 & -x_{e} \\ 0 & 1 & 0 & -y_{e} \\ 0 & 0 & 1 & -z_{e} \\ 0 & 0 & 0 & 1\end{array}\right]\)
  • Difficult to directly get $R_{view}$, so consider its inverse rotation:
    \(R_{v i e w}^{-1}=\left[\begin{array}{cccc}x_{\hat{g} \times \hat{t}} & x_{t} & x_{-g} & 0 \\ y_{\hat{g} \times \hat{t}} & y_{t} & y_{-g} & 0 \\ z_{\hat{g} \times \hat{t}} & z_{t} & z_{-g} & 0 \\ 0 & 0 & 0 & 1\end{array}\right] \quad \Rightarrow \quad R_{v i e w} = (R_{v i e w}^{-1})^{T} = \left[\begin{array}{cccc}x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\ x_{t} & y_{t} & z_{t} & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1\end{array}\right]\)

Tip: We can validate the result of the multiplication of $R_{v i e w}^{-1}$ and the vector $\left(\begin{array}{llll}1 & 0 & 0 & 0\end{array}\right)$ which represents $X$ axis, the vector $\left(\begin{array}{llll}0 & 1 & 0 & 0\end{array}\right)$ which represents $Y$ axis, and the vector $\left(\begin{array}{llll}0 & 0 & 1 & 0\end{array}\right)$ which represents $Z$ axis. We could find $X$ axis rotates to $\hat{g} \times \hat{t}$, $Y$ rotates to $t$ and $Z$ rotates to $-g$.

Note: Each column of the $R_{view}$ except for the last column is the unit vector describing the camera, so the transposed matrix of it is its inversed matrix itself.

Projection transformation

Projection in Computer Graphics

• In orthogonal projection, the camera can be supposed to be placed infinite way from the viewing frustum (now the frustum becomes cuboid).

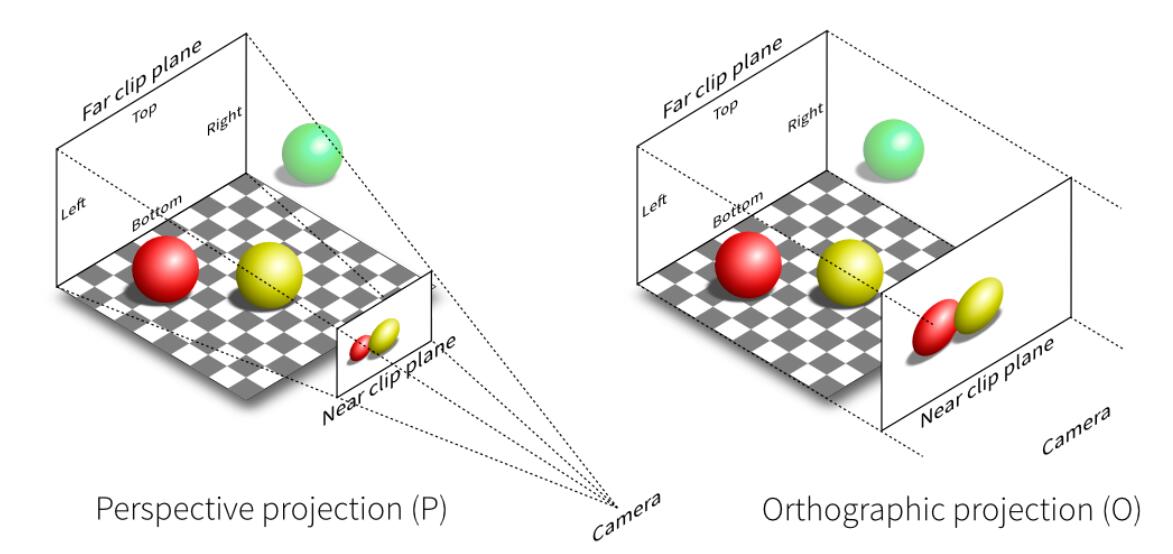
Orthographic Projection

• Camera located at origin, looking at -Z, up at Y
• Drop Z coordinate
• Translate and scale the resulting rectangle to $\left[-1, 1\right]^2$

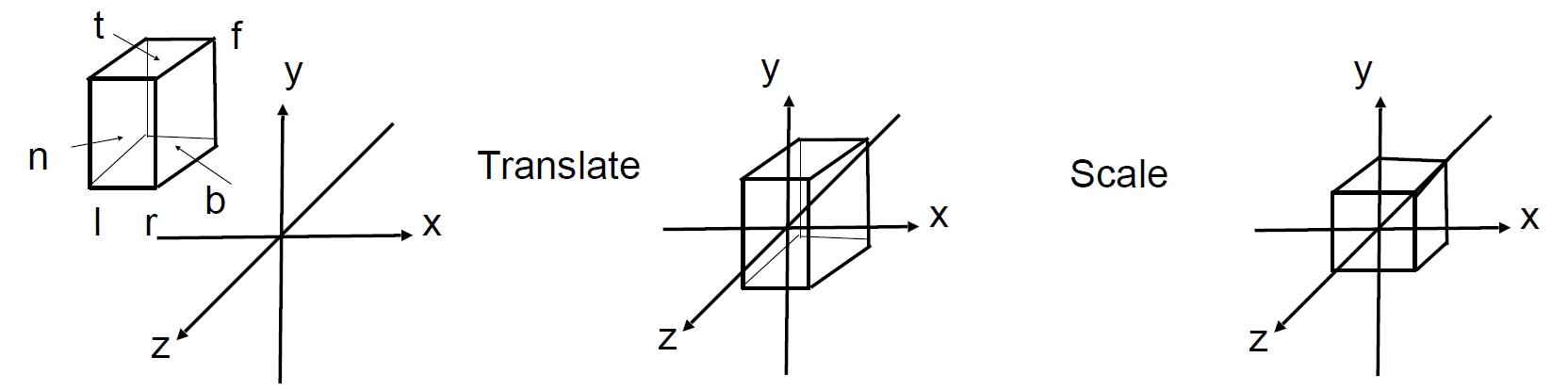
• More in general: map a cuboid $\left[l, r\right] \times \left[b, t\right] \times \left[f, n\right]$ to the canonical cube $\left[-1, 1\right]^3$. (left, right, bottom, top, far, near)
  • Translate the center to origin first, then scale each edge to 2.

\[M_{\text {ortho}}=\left[\begin{array}{cccc}\frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1\end{array}\right]\left[\begin{array}{cccc}1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1\end{array}\right]\]

Note: Objects may be stretched out of the original scale, so the next viewport transform will deal with this and draw it back to the original scale.

Caveat: Looking along $-Z$ makes n > f (near > far) and this is the reason why OpenGL uses left hand coords.

Perspective Projection

• Most common in Computer Graphics, art, visual system
• Further objects are smaller
• Parallel lines not parallel, converge to single point

Note: We only consider Euclidean Geometry (Not Riemannian Geometry)

The step to do perspective projection

1. First squish the frustum into a cuboid $M_{\text {persp} \rightarrow \text {ortho}}$
2. Do orthographic projection $M_{ortho}$

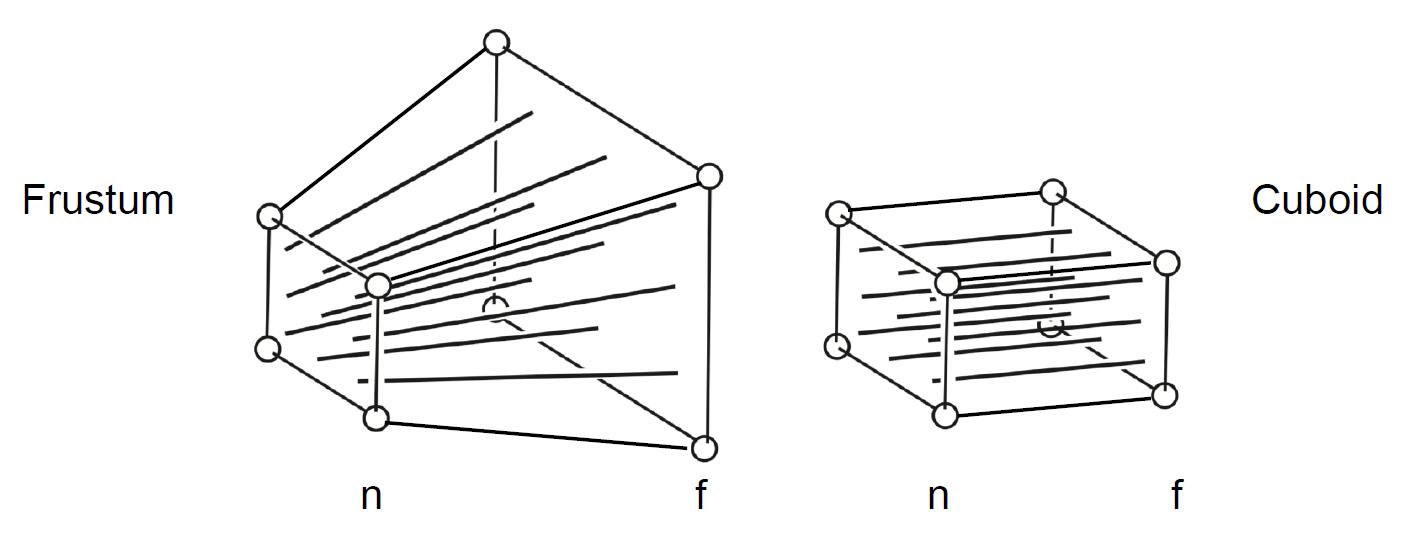
• Denote vertical field-of-view (fovY) and aspect ratio (assume symmetry i.e. $l=-r\ b=-t$)

\[Aspect\ Ratio=\frac{width}{height}\]

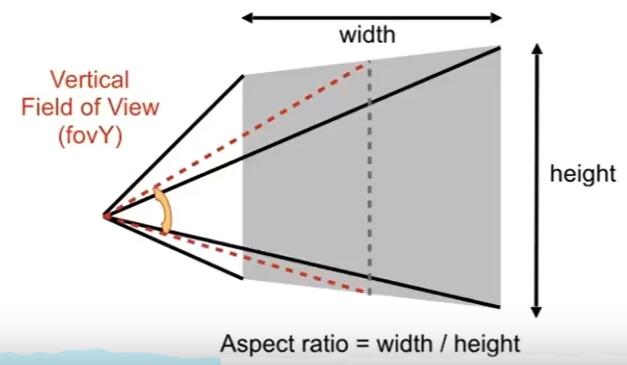
• Convert fovY and aspect to l, r, b, t

\[\begin{aligned} \tan \frac{f o v Y}{2} &=\frac{t}{|n|} \\ \text { aspect } &=\frac{r}{t} \end{aligned}\]

• Find the relationship between transformed points $\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$ and original points $\left(x, y, z)\right)$

\[y^{\prime}=\frac{n}{z} y\]

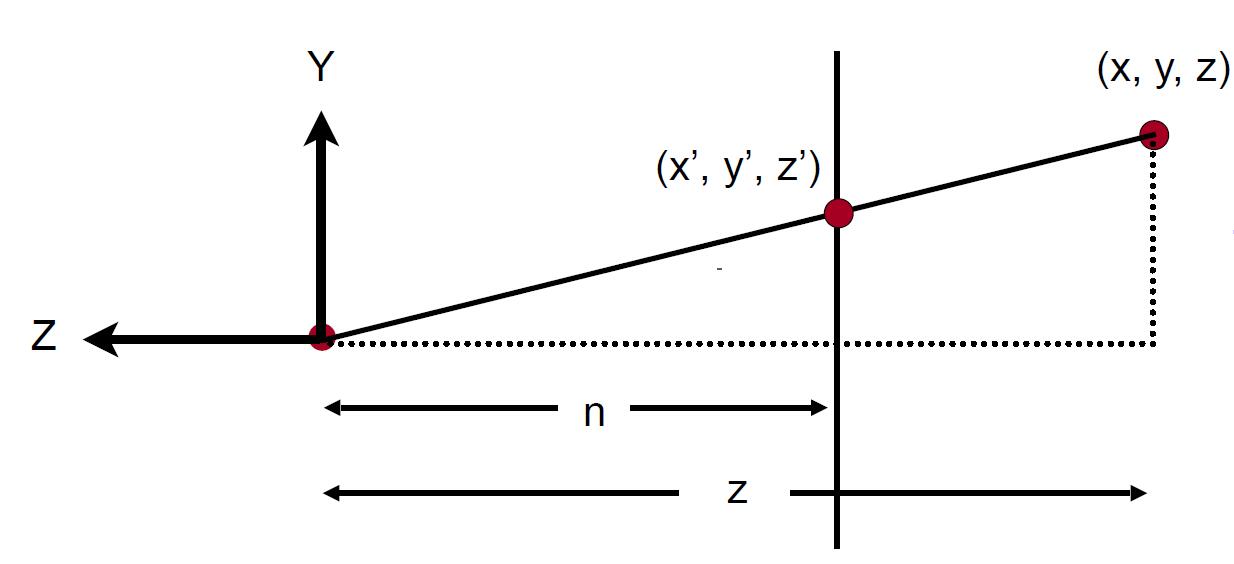
Similar to $x$:

\[x^{\prime}=\frac{n}{z} x\]

• Use homogenous coordinates to represent this relationship:

\[\left(\begin{array}{l}x \\ y \\ z \\ 1\end{array}\right) \Rightarrow\left(\begin{array}{c}n x / z \\ n y / z \\ \text { unknown } \\ 1\end{array}\right) \begin{array}{l} == \end{array}\left(\begin{array}{c}n x \\ n y \\ \text { still unknown } \\ z\end{array}\right)\]

Tip: according to the points defined in homogenous coordinates. reference

• So the operation squish should be the following form:

\[M_{\text {persp} \rightarrow \text {ortho}}^{(4 \times 4)}\left(\begin{array}{l}x \\ y \\ z \\ 1\end{array}\right)=\left(\begin{array}{c}n x \\ n y \\ \text { unknown } \\ z\end{array}\right)\]

• Three known parameters could get a good reference of three rows of $M_{\text {persp} \rightarrow \text {ortho}}$:

\[M_{\text {persp} \rightarrow \text {ortho}}=\left(\begin{array}{cccc}n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0\end{array}\right)\]

• Two important observations, which is responsible for $z^{\prime}$:

1. Any point on the near plane will not change

\[M_{\text {persp} \rightarrow \text {ortho}}^{(4 \times 4)}\left(\begin{array}{l}x \\ y \\ z \\ 1\end{array}\right)=\left(\begin{array}{c}n x \\ n y \\ \text { unknown } \\ z\end{array}\right) \quad \begin{array}{l}\end{array}\]

Replace $z$ with $n$:

\[\left(\begin{array}{l}x \\ y \\ n \\ 1\end{array}\right) \Rightarrow\left(\begin{array}{l}x \\ y \\ n \\ 1\end{array}\right)==\left(\begin{array}{c}n x \\ n y \\ n^{2} \\ n\end{array}\right)\]

Thus, the third row must be of the form $(0\ 0\ A\ B)$:

\[\left(\begin{array}{llll}0 & 0 & A & B\end{array}\right)\left(\begin{array}{l}x \\ y \\ n \\ 1\end{array}\right)=n^{2}\] \[A n+B=n^{2}\]

Tip: $n$ is only the known paramter, and has nothing to do with $z$, so $A$ and $B$ can not be determined yet.

2. Any $z$ of points on the far plane will not change

\[\left(\begin{array}{l}0 \\ 0 \\ f \\ 1\end{array}\right) \Rightarrow\left(\begin{array}{l}0 \\ 0 \\ f \\ 1\end{array}\right)==\left(\begin{array}{l}0 \\ 0 \\ f^{2} \\ f\end{array}\right)\] \[A f+B=f^{2}\]

• From the two above equations we get, we could solve $A$ and $B$:

\[\left\{\begin{array}{l}A n+B=n^{2} \\ A f+B=f^{2}\end{array}\right. \Rightarrow \left\{\begin{array}{l}A=n+f \\ B=-n f\end{array}\right.\]

• Now, every entry of $M_{\text {persp} \rightarrow \text {ortho}}$ is known:

\[M_{\text {persp} \rightarrow \text {ortho}}=\left(\begin{array}{cccc}n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0\end{array}\right)\]

• Finally, do orthographic projection $M_{ortho}$ to finish

• In summary: $M_{\text {persp}}=M_{\text {ortho}} M_{\text {persp} \rightarrow \text {ortho}}$

Reference

• GAMES101, Lingqi Yan
• 如何通俗地解释欧拉角？
• 欧拉角与万向节死锁