Whitted Style Ray Tracing, Ray-Surface Intersection, Acceleration of Ray Tracing, Ray-Intersection with AABB, KD-Tree, BVH
Ray Tracing
- Rasterization can not handle global effect well
- Soft shadows
- Glossy reflection, transparent / subtransparent object
- Indirect illumination when light bounces more than once
- Ray tracing is accurate, but is very slow
- Rasterization: real time, Ray tracing: offline
- Time estimation: ~10K CPU core hours to render one frame in video production
Light Rays
- Three ideas about light rays:
- Light travels in straight lines, though this is wrong because light is a wave which has volatility.
- Light rays do not collide with each other if they cross, though this is still not wrong.
- Light rays travel from the light sources to the eye, and the reciprocity of the light means the physics is invariant under path reversal.
Ray Casting
-
Pinhole Camera Model
-
Generate an image by casting one ray per pixel
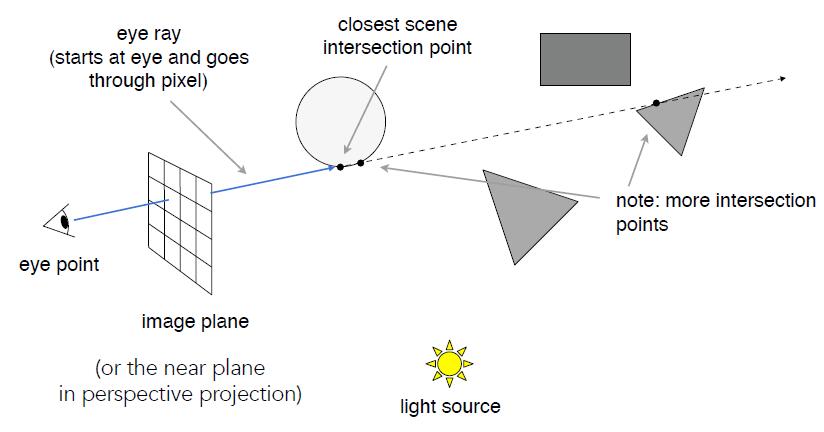
- Check for shadows by sending a ray to the light
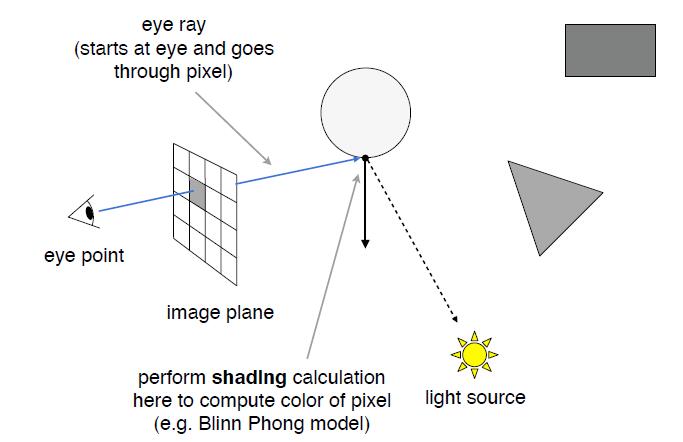
- Whitted-Style Ray Tracing: Recursive Ray Tracing
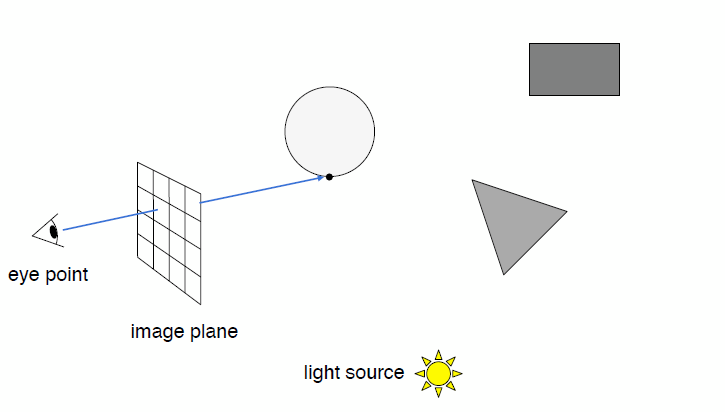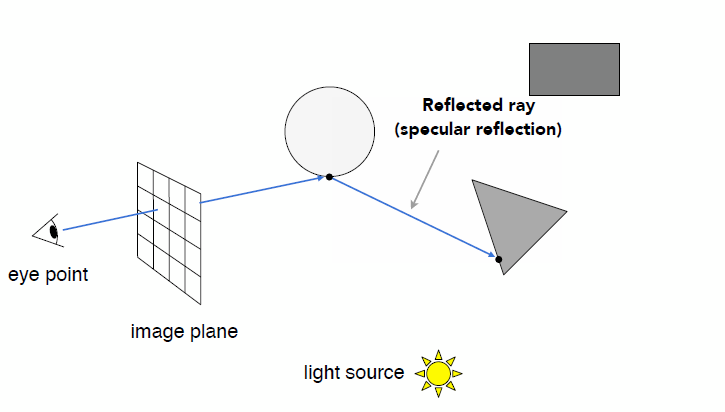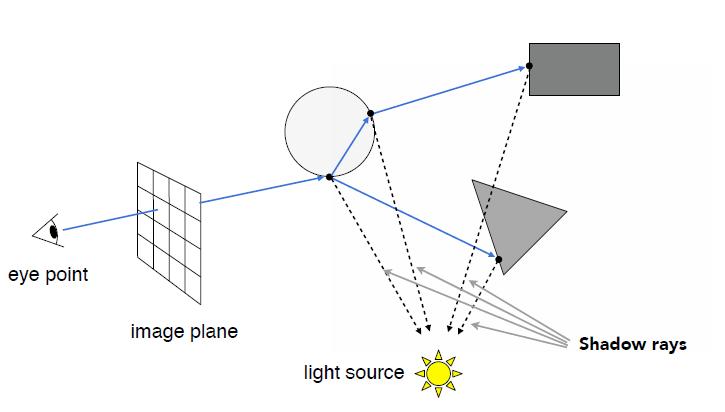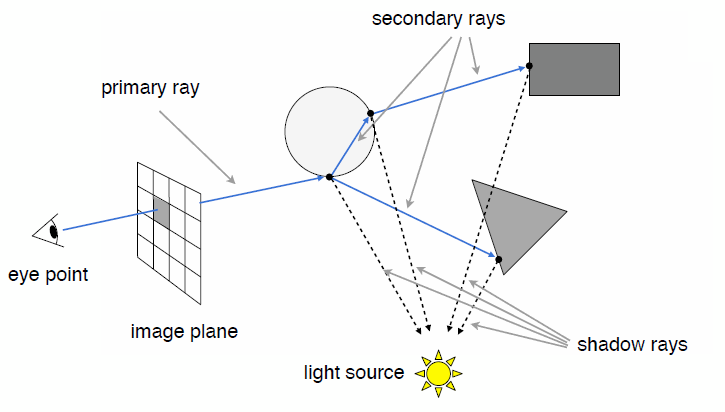
- Key idea: ray tracing is to simulate the ray casting
Ray-Surface Intersection
Ray Equation
- Ray is defined by its origin and a direction vector
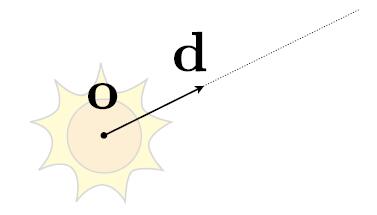
- Ray equation $\boldsymbol{r}(t) = \boldsymbol{o} + t\boldsymbol{d}$ where, $0 \leq t < \infty$
- $o$: origin point
- $d$: normalized direction of the ray
- $r(t)$: point along the ray
Intersect with Sphere
- Ray: $\boldsymbol{r}(t) = \boldsymbol{o} + t\boldsymbol{d}, 0 \leq t < \infty$
- Sphere: $ \boldsymbol{p}:\ (\boldsymbol{p}-\boldsymbol{c})^2-R^2 = 0$
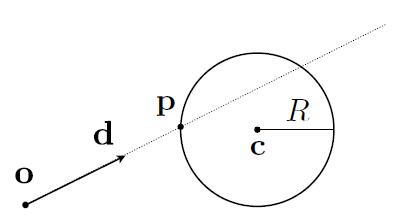
- The intersection $p$ must satisfy both ray equation and sphere equation
- Intersection: $ (\boldsymbol{o}+ t\boldsymbol{d}-\boldsymbol{c})^2-R^2 = 0$
- Ray intersects with sphere if only if $\varDelta \ge 0$ and $t \ge 0$, otherwise no intersection.
- Given the solved $t$, intersection is $\boldsymbol{o} + t\boldsymbol{d}$.
Intersect With Implicit Surface
- Ray: $\boldsymbol{r}(t) = \boldsymbol{o} + t\boldsymbol{d}$, where $0 \leq t < \infty$
- General implicit surface: $\boldsymbol{p}: f(\boldsymbol{p}) = 0$
- Substitute ray equation: $f(\boldsymbol{o}+t\boldsymbol{d}) = 0$
- Solve for real, positive roots of $t$
Info: we usually don’t care about how to solve the equation, because numerical optimization will always help us to find an approximate solution of the problem corresponding to the given equation of implicit surface.
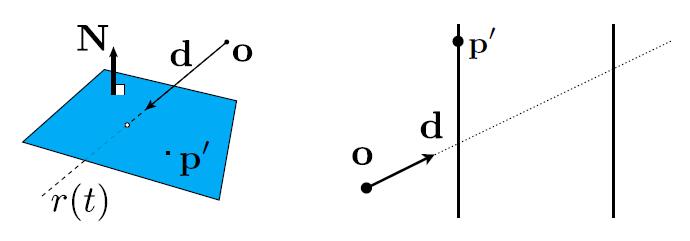
Plane Equation
- Plane is defined by normal vector and a point on plane
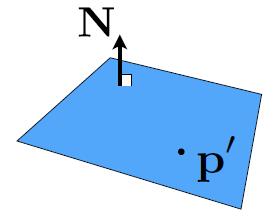
- Plane Equation: $\boldsymbol{p}: (\boldsymbol{p}-\boldsymbol{p^\prime}) \cdot \boldsymbol{N}=0$
- $p$: all points on plane
- $p^\prime$: one point on plane
- $N$: normal vector
- Expland the plane equation will get Plane Equation in Cartesian coordinates: $ax + by + cz + d = 0$
- Solve for intersection
- Set $\boldsymbol{p} = \boldsymbol{r}(t)$ and solve for $t$
- Check if $0 \leq t<\infty$ intersection inside the plane, otherwise not.
- After get the $t$ and intersection with the plane, check if the intersection is inside triangle
- Use three cross product and check if the results are all in the same direction
Intersect with Triangle Mesh
- Usage: visiblity, shadows, lighting …
- Geometry: inside / outside test
Tip: Point in Polygon test is: given a point $p$ and a polygon $Q$, draw a line from the query point $p$ to other point far away in the plane, which should be outside $Q$, then count the number of intersection of this ray with $Q$. If odd number of intersections, the point $p$ is inside polygon $Q$, otherwise outside.
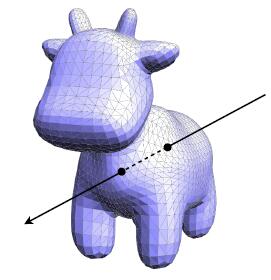
- Idea: just intersect ray with each triangle
- Simple, but very slow since for each resolution pixel of the screen will cast a ray and do intersection test with each triangle in mesh
-
Only care 0, 1 intersection, ignore multiple edge cases
- Triangle is in a plane
- Ray-plane intersection
- Test if hit point is inside triangle
- Möller Trumbore Algorithm
- Given barycentric coordinate of triangle, a faster and direct approach to calculate intersection
- Use Cramer’s rule to solve for system of linear equations
- The proof can be found here
- After get $t$, $b_1$,\ $b_2$
- Check if $t \ge 0$ then the intersection is in the plane, otherwise not
- Check if $0 \le b_1,\ b_2,\ 1-b_1-b_2 \le 1$ then the intersection is inside triangle, otherwise not
- If both conditions are satisfied, the ray does intersect with the triangle
Acceleration
- Simple ray-scene intersection
- Exhaustively test ray-intersection with every triangle
- Find the closest hit
- Problem
- Naive algorithm = num_pixels x num_triangles x num_bounces
- Very slow
Bounding Volumes
- Quick way to avoid intersections: bound complex object with a simple volume
- Object is fully contained in the volume
- If it doesn’t hit the volume, it doesn’t hit the object
- Thus, test bounding volume first, then test object if it hits

Ray-Intersection With Box
-
Box is the intersection of 3 pairs of slabs
-
Axis-Aligned Bounding Box (AABB): the smallest enclosing box with any side along either x, y, z axis.
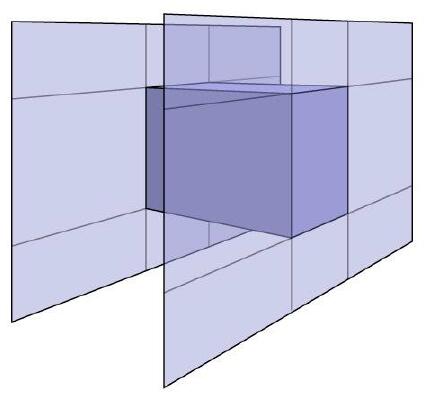
- ‘Axis-Aligned’ is to reduce computational time
- For the general plane, 3 subtractions, 6 multiplies, 1 division required
\(t=\frac{\left(\mathbf{p}^{\prime}-\mathbf{o}\right) \cdot \mathbf{N}}{\mathbf{d} \cdot \mathbf{N}} \quad\) - For slabs perpendicular to x-axis, only 1 subtraction, 1 division required
\(t=\frac{\mathbf{p}^\prime_x - \mathbf{o}_x}{\mathbf{d}_x}\)
- For the general plane, 3 subtractions, 6 multiplies, 1 division required
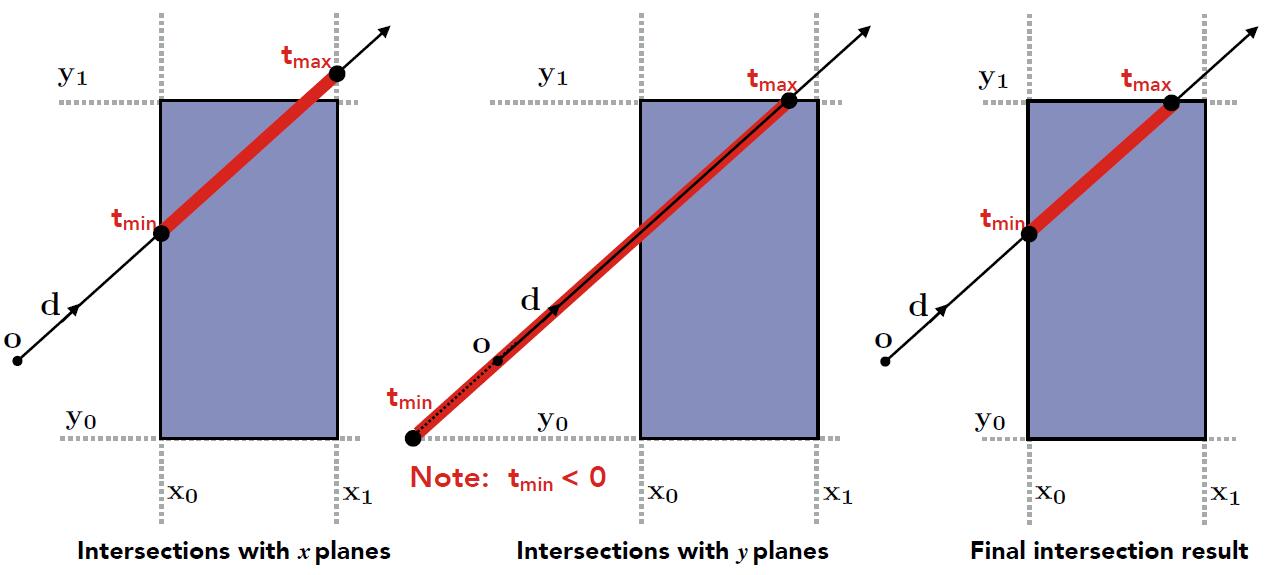
Intersect with 2D AABB
- 2D example of computing intersections with slabs and take intersection of $t_{min}/ t_{max}$ intervals
Intersect with 3D AABB
- A box in 3D = three pairs of infinitely large slabs
- Key ideas
- The ray enters the box only when it enters all pairs of slabs
- The ray exits the box as long as it exits any pair of slabs
- For each pair, calculate the $t_{min}$ and $t_{max}$. Negative is fine and will be discussed later
- For the 3D box, $t_{enter} = max \{ t_{min} \}$, $t_{exit} = min \{ t_{max} \} $
- If $t_{enter} \lt t_{exit}$, we know the ray stays a while in the box, thus ray must intersect with bounding box. But this is NOT absolutely correct!
- e.g. the following ray won’t intersect with the bounding box
- Problem: what about the $t$ is negative?
- Ray is not a line, but a ray
- Should check whether $t$ is negative for physical correctness
- What if $t_{exit} \lt 0$
- The box is behind the ray: no intersection
- What if $t_{exit} \ge 0$ and $t_{enter} \lt 0$
- The ray’s origin is inside the box: have intersection
- In summary, ray and AABB intersect if and only if
- $t_{enter} \lt t_{exit} 0\ \&\&\ t_{exit} \ge 0$
Uniform Spatial Partitions
- Preprocess to build acceleration grid
- Find bounding box
- Create grid
- Store each object in overlapping cells (test if the object’s surface intersects with cells)
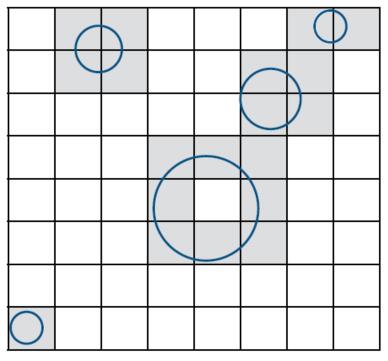
- Ray Scene Intersection
- Step through grid in ray traversal order
- For each grid cell
- Test intersection with all objects stored at that cell
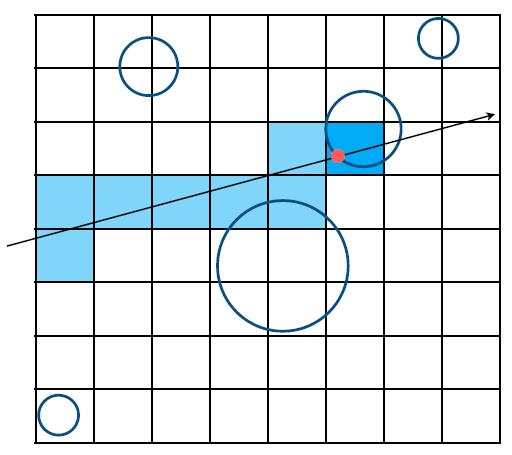
- Grid resolution should not be too small nor too large
- One cell: no speedup
- Many cells: infficiency due to extraneous grid traversal
- Heuristic experience
- num_cells = Const * num_objs
- Const ≈ 27 in 3D
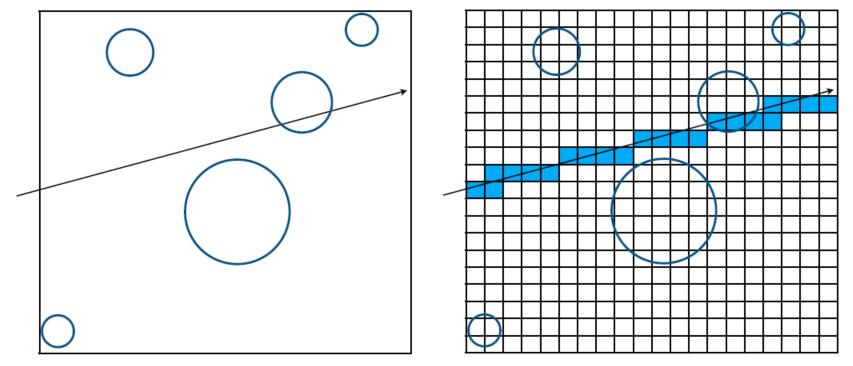
- Uniform Grids’ Problem
- Work well on large collections of objects that are distributed evenly in size and space
- But fail on the scene where large ratio of space is empty with no objects or the objects are not evenly distributed, i.e. “Teapot in a stadium” problem
- Spatial Partition to solve this problem!

Spatial Partitions
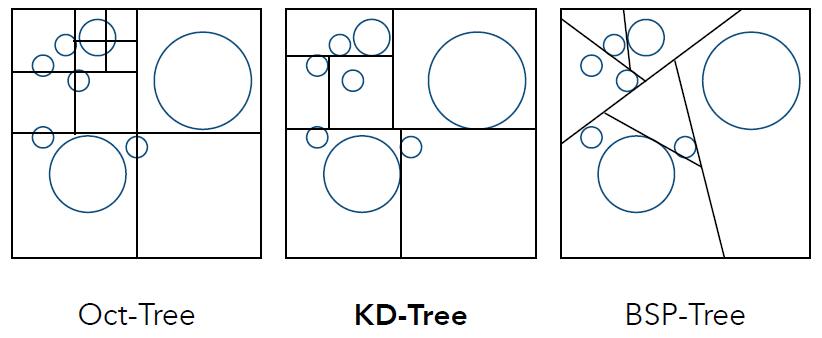
- Partition the 3D space using plane
- Oct-Tree: Recursively partition the space into 8 subspace until specified condition, e.g. the new splitted cells are empty with no objects
- KD-Tree (short for k-dimensional tree): Alternatively use xy-plane, yz-plane, xz-plane to divide objects into different space
- BSP-Tree (short for binary space partitioning tree): More general case of KD-Tree. Recursively subdividing a space into two subspace
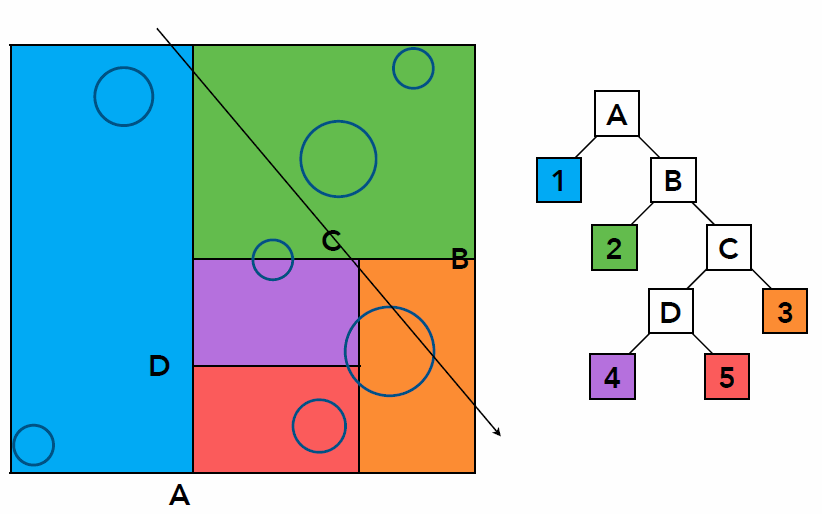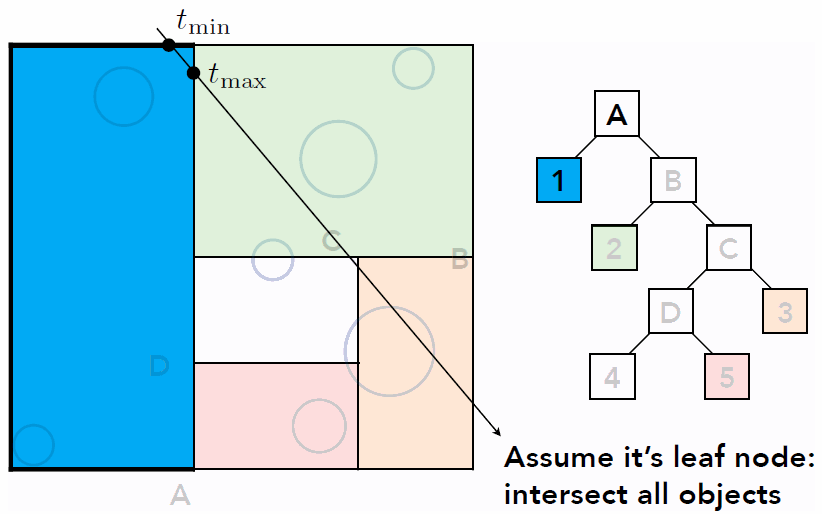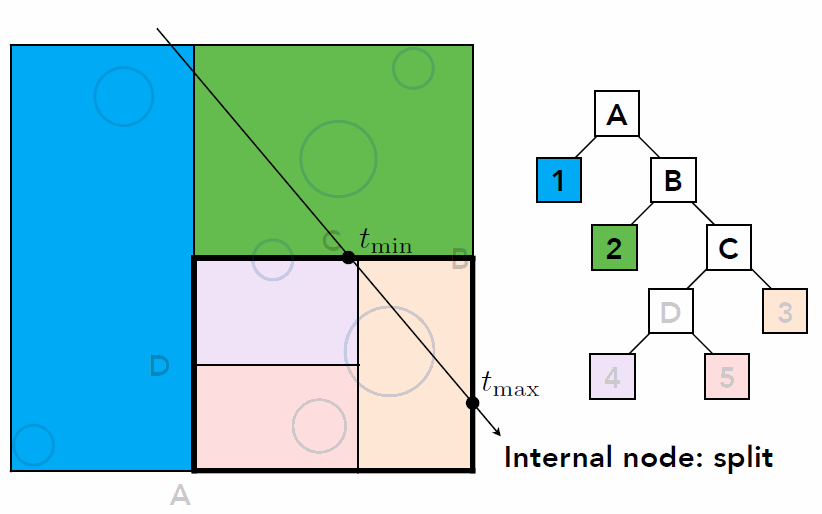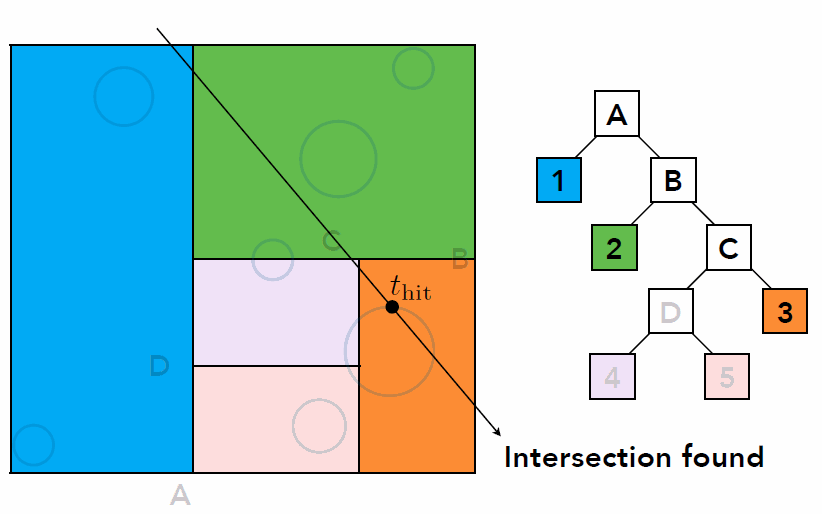
- Data Structure for KD-Tree
- Internal Nodes store
- split axis: x-, y-, or z-axis
- split position: coordinate of split plane along axis
- children: pointers to child nodes
- No objects are stored in internal nodes
- Leaf nodes store
- list of objects
- Internal Nodes store
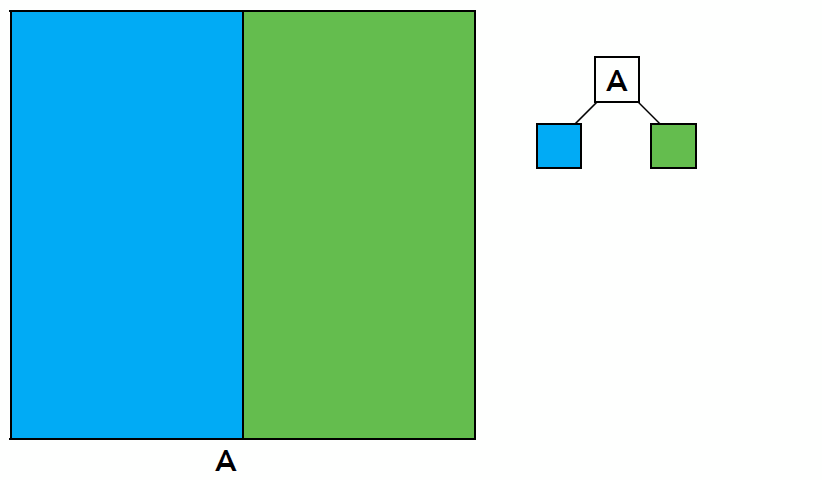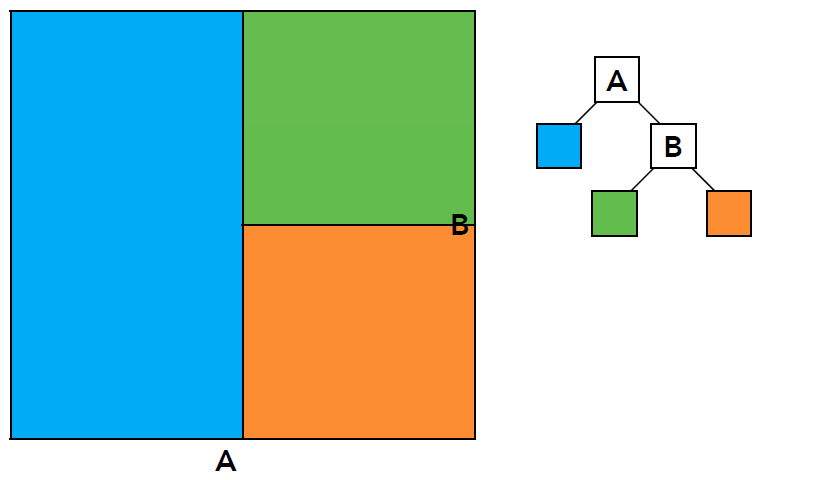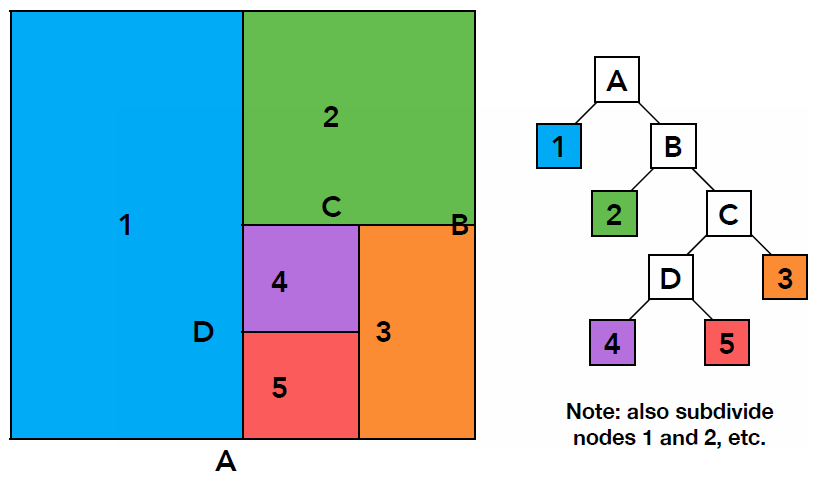
- Traversing a KD-Tree
- Problem existed in KD-Tree method
- Computing the overlap between triangle and AABB to build KD-Tree is difficult, though intersection algorithm exist, detailed here
- One objects can be included in multiple cells
Object Partitions
- Bounding Volume Hierarchy (BVH): tree structure on a set of geometric objects, which are wrapped in bounding volumes
- Find bounding box
- Recursively split set of objects in two subsets
- Recompute the bounding box of the subsets
- Stop when necessary
- Store objects in each leaf node
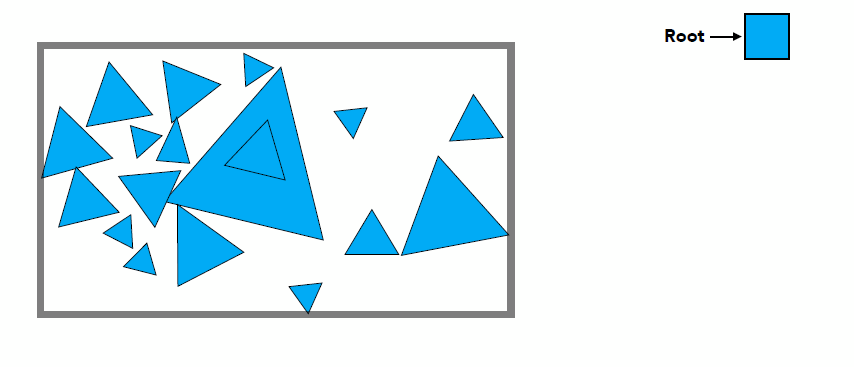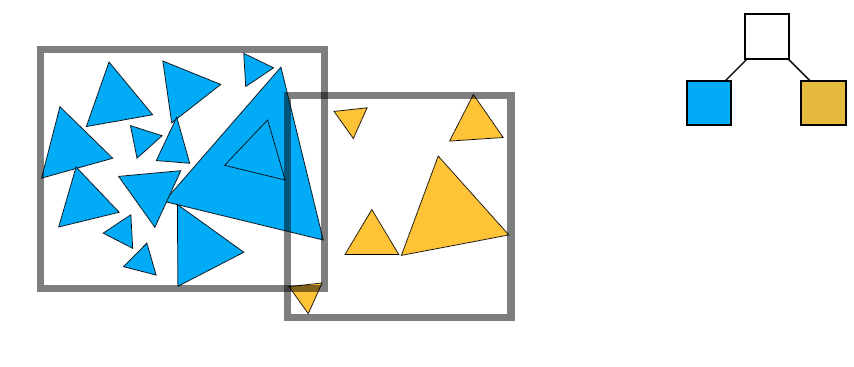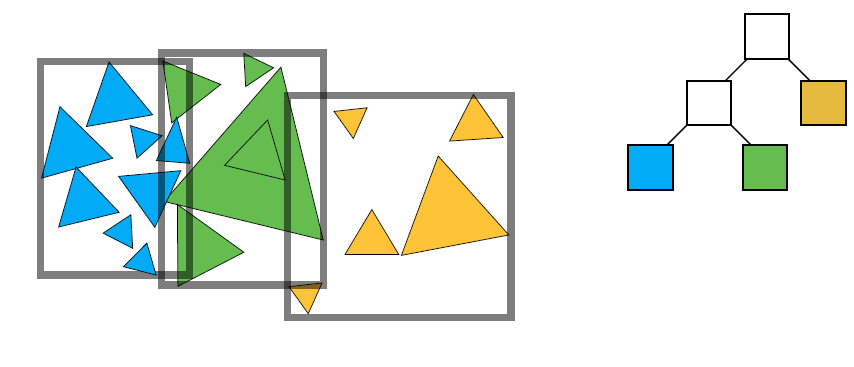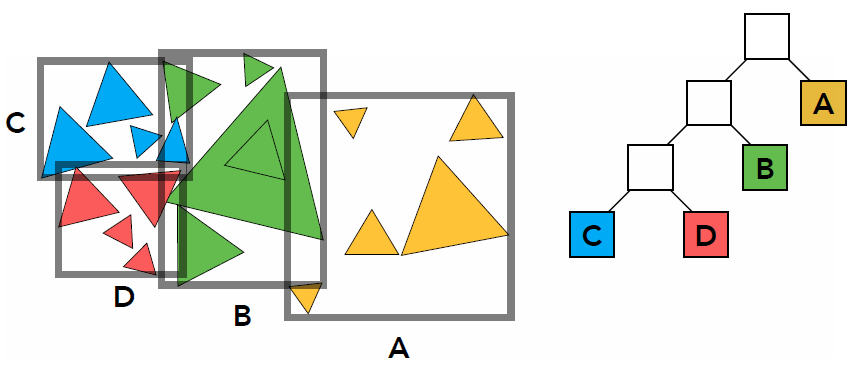
- The problem existed in KD-Tree are solved
- No need to compute the overlap because overlap doesn’t influence, but precompute the bounding box which may overlap one another
- One object only exist in one node
- BVH is the preprocess to accelerate unnecessary computation before ray tracing and shading, but for each time the objects move or displace to somewhere else, BVH will be built once again for each frame. Thus, Real-time ray tracing is great difficult.
- Thus it is hard for real-time ray tracing to deal with shape deformation and position transformation, since it is great time-costly to build accelerating structure
- Strategy to subdivide a node to build BVH
- Choose a dimension to split: Always choose the longest axis in node, especially when objects in elongated bounding box
- Choose split position: Split node at location of median object, which is beneficial to build a more balanced tree with more evenly depth of two side.
- Termination criteria: stop when node contains few elements (e.g. heuristically 5)
Tip: Choosing split position of median object can be implement by sorting the barycentric of each triangle and select the median one, which take $O(nlog(n))$ time. While quick selection algorithm for finding the kth smallest value can optimize the consuming complexity to $O(n)$.
- Data Structure for KD-Tree
- Internal nodes store
- Bounding box
- Children: pointers to child nodes
- Leaf nodes store
- Bounding box
- List of objects
- Internal nodes store
- Traversing BVH
Intersect(Ray ray, BVH node) {
if (ray misses node.bbox)
return;
if (node is a leaf node){
test intersection with all objects;
return closest intersection;
}
hit1 = Intersect(ray, node.child1);
hit2 = Intersect(ray, node.child2);
return the closer of hit1, hit2; // ATTENTION: closer hit point is returned!
}
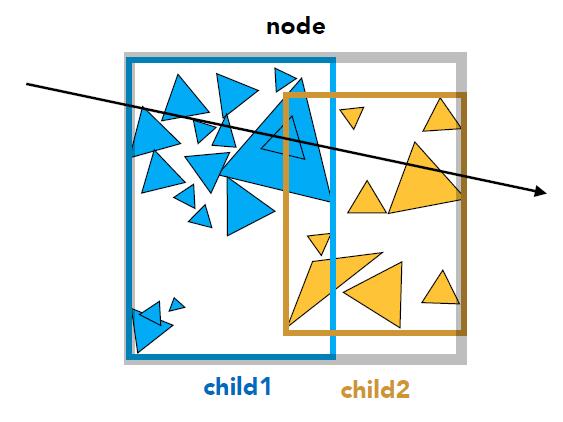
Spatial vs Object Partitions
- Spatial partition (e.g. KD-Tree)
- Partition space into non-overlapping regions
- Object can be contained in multiple regions
- Object partition (e.g. BVH)
- Partition set of objects into disjoint subsets
- Bounding boxes for each set may overlap in space