Shading, Blinn-Phong Shading Model, Shading Frequency, Shadow Mapping, Graphics Pipeline
Shading
What we done so far
- Model transformation
- View transformation
- Projection transformation
- Viewport transformation
- Rasterization
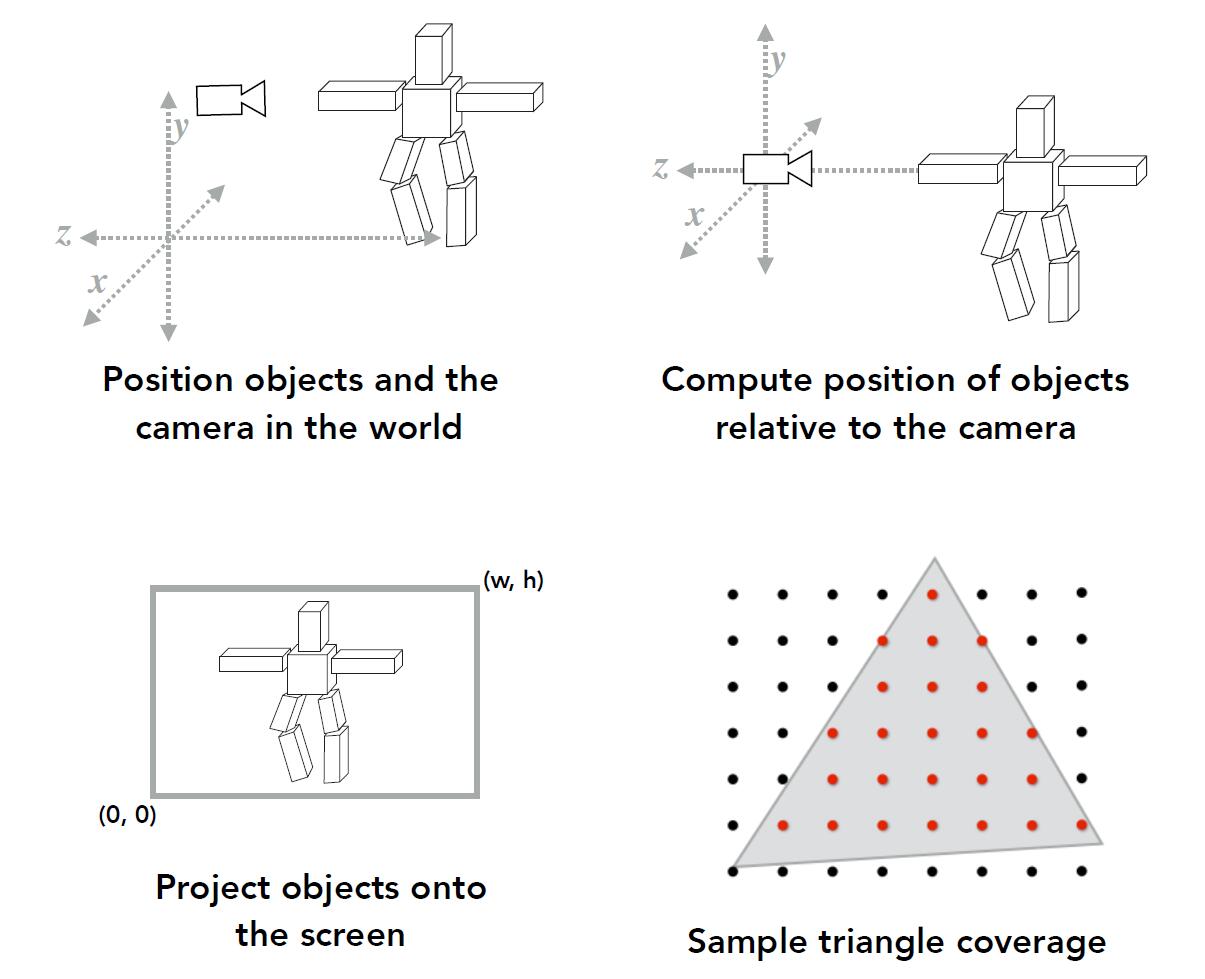
- The color applied to each pixel has not been determined yet.
Blinn-Phong Reflectance Model
Shading: The process of applying a material to an object.
- Specular highlight: the bright spot of light that apperas on shiny objects when illuminated. Direct light
- Diffuse lighting: when a surface that faces an angle 90 degrees or less of the light, it will get a percentage of the light source. Direct light, but diverted from the light source
- Ambient lighting: light of the environment, most of which comes from reflected surfaces (by diffusion). Indirect light and not in the path of light source
Tip: We often assume ambient lighting is a constant.

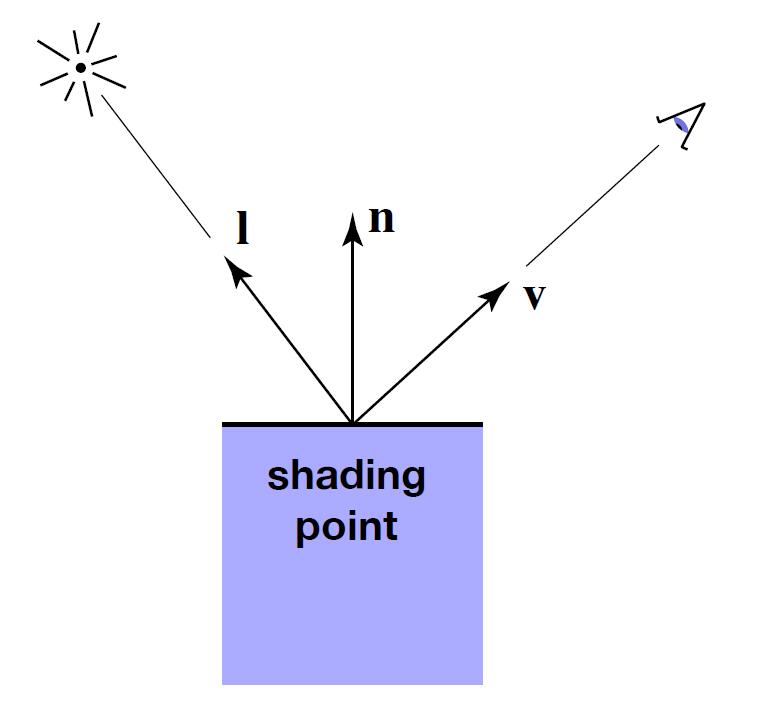
Shading point
- Compute light reflected toward camera at a specific shading point
- Inputs:
- Viewer direction $v$
- Surface normal $n$
- Light direction $l$
- Surface parameters, properties (color, shininess, etc.)
Caveat: Above are all unit vectors.
-
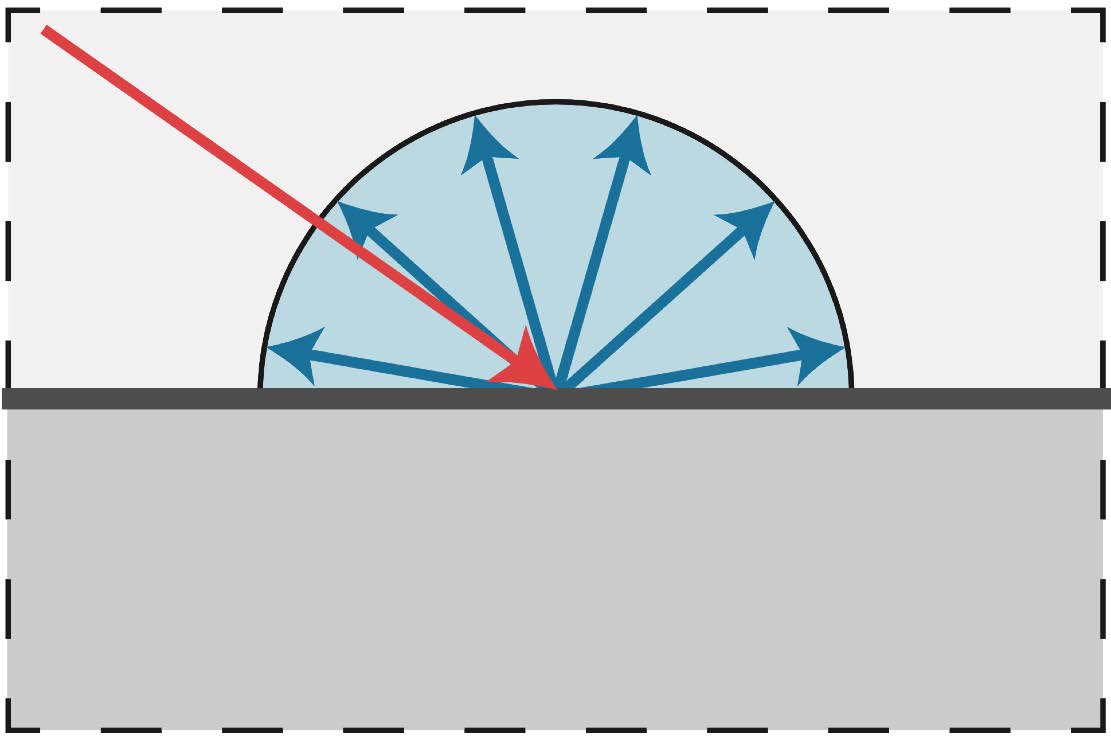
Shading is local, so No Shadows will be generated! (shading ≠ shadow)
-
The below region in red rectangular is blocked by the object from the light source, but we still shade color to it since shading is local. The shadow of this area will be discussed later

Blinn-Phong Model
Diffuse reflection
- Light is scattered uniformly in all directions
- Surface color is the same for all viewing directions
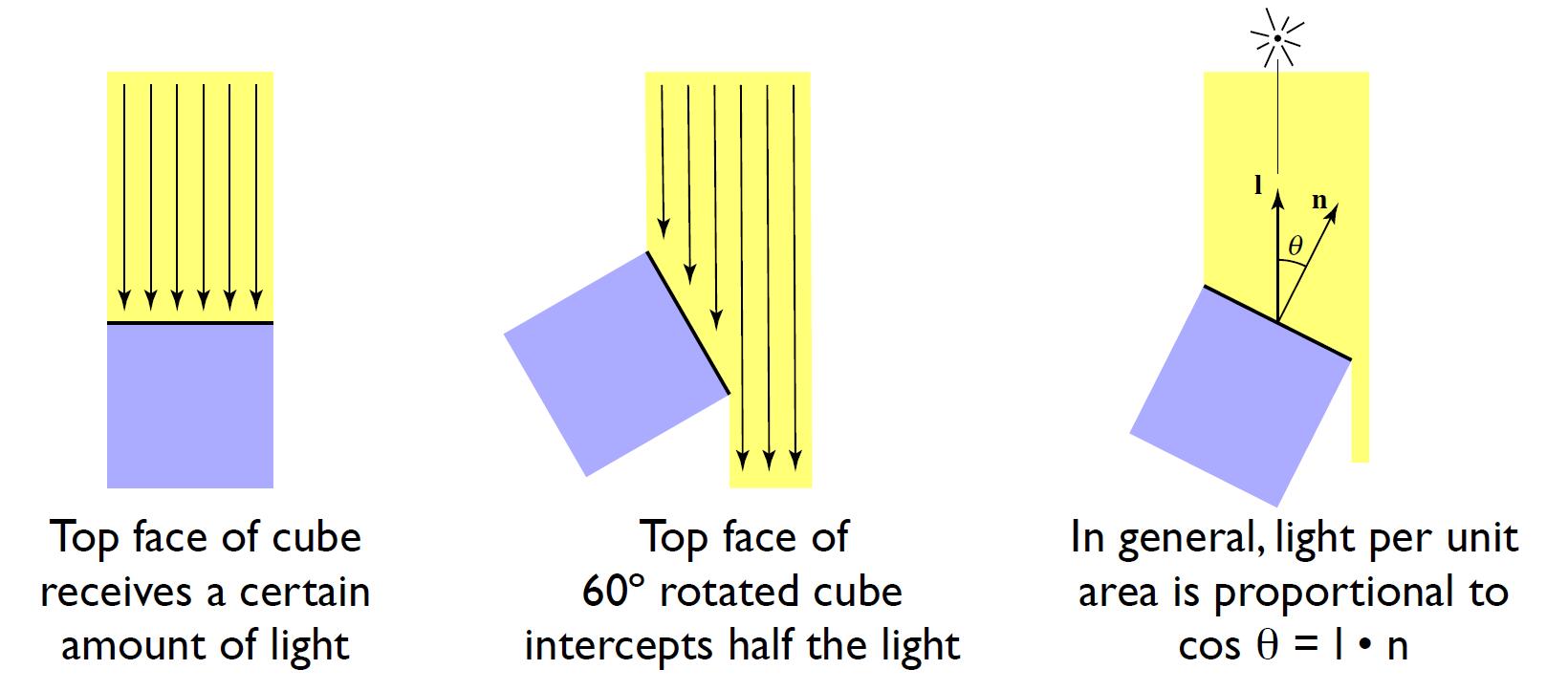
- Lambert’s cosine law: determine how much light is received
Light Falloff
- Assume that ideally there is no loss of energy, for each moment of energy transmission, each spherical shell carries the same amount of luminous energy. For each unit space $dS$ on the spherical shell, we assume the energy is the same, so the for each spherical shell, the total amount of energy is $\oint IdS = 4\pi r^2 I$. Thus $I$ is inversely proportional to the square of the distance $r$.
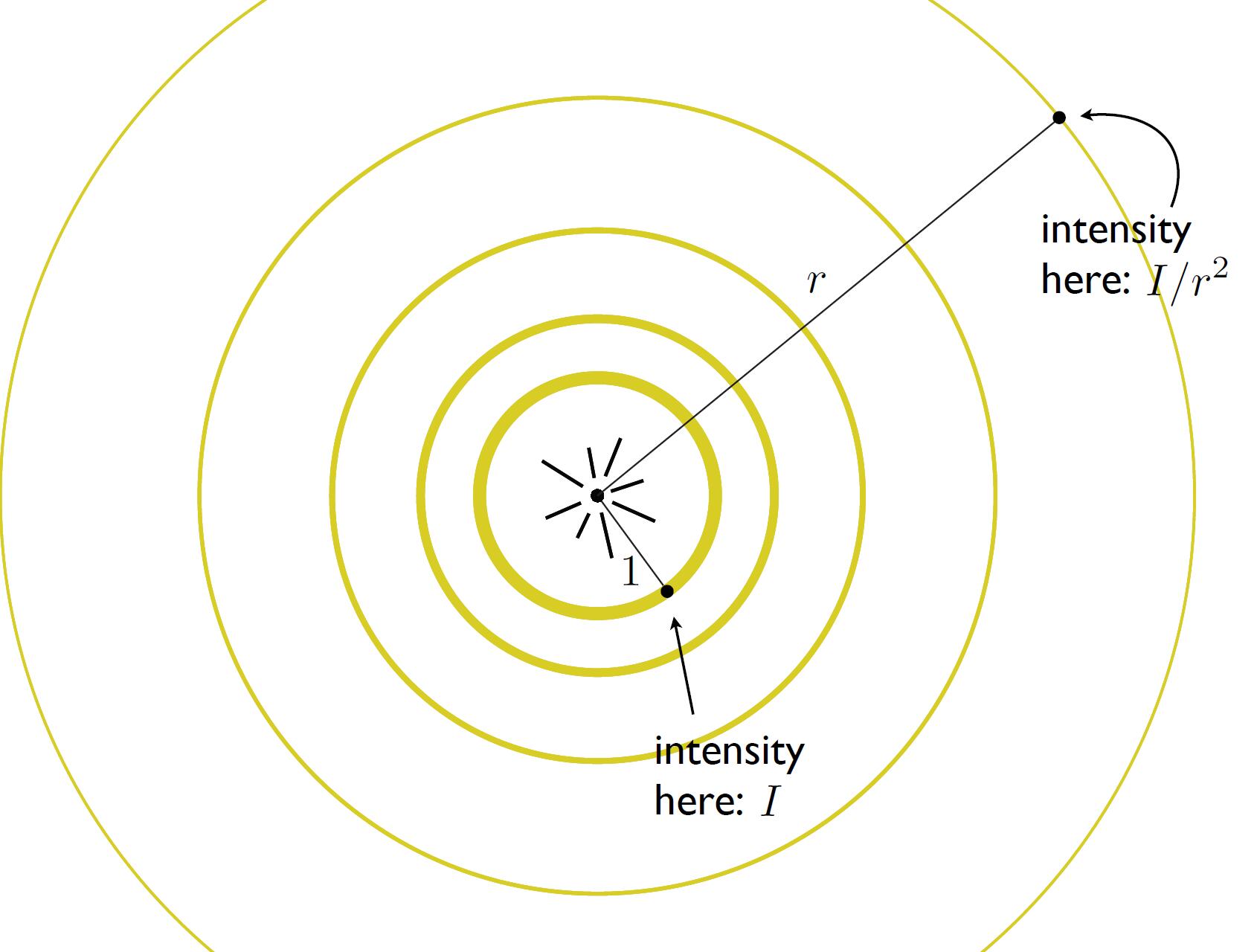
Note: Above proof is not strict, but intuitive. More strict prove is as follows: We assume there is no energy loss, so the luminous energy $Q$ from the light source per unit time is the same. According to $\Phi = dQ / dt$, we can get the luminous flux $\Phi$ per time unit is the same. From the definition of luminance: $L_{v} = d^2\Phi / d\Omega dA cos\theta$, the total of luminance $4\pi r^2 L_{v} = d\Phi / d\Omega cos\theta$ should be the same. Thus luminance $L_{v}$ is inversely proportional to the square of the distance $r$.
Caveat: More detail and the relationship between Luminous intensity $l_{v}$ and Luminance $L_{v}$ will be discussed in Radiometry part.
Diffuse Term
-
Lambertian Shading (Diffuse shading)
-
Shading independent of view direction $v$
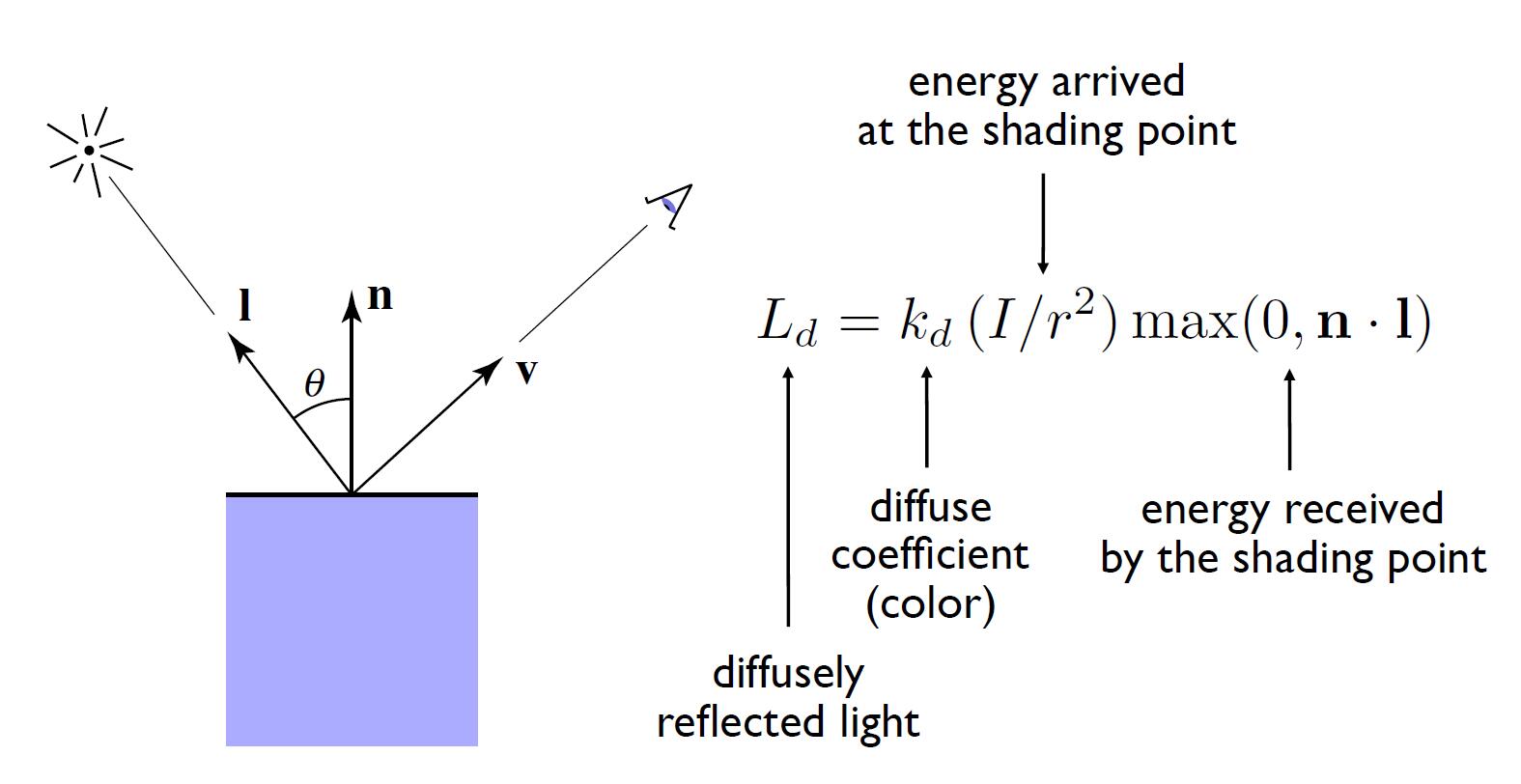
- $\max (0, \mathbf{n} \cdot \mathbf{l})$ is to ensure the shading value is always positive even if the light comes from the back of the object
info: The energy received is relative to the angle between normal $n$ and light $l$. This is also the reason why we feel cold in winter and hot in summer.
- Diffuse coefficient: often defined as 3 or 4 dimensional vector to store the percentage of energy the shading point reflects (not absorb in). Indirectly contain the material information of the object.

Specular Term
- Intensity depends on view direction
- Specular highlight close to mirror reflection direction
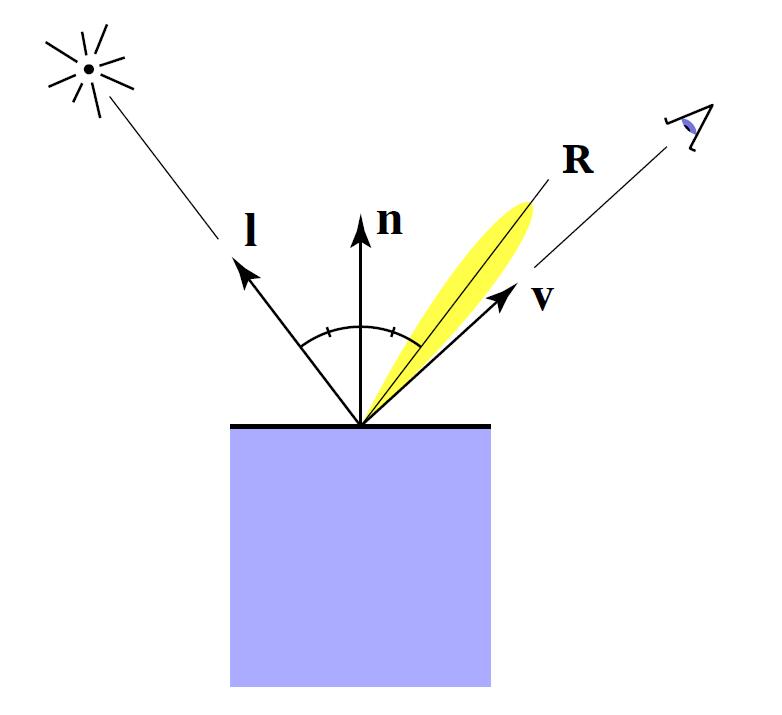
- $v$ close to mirror direction $\Leftrightarrow$ half vector close to normal
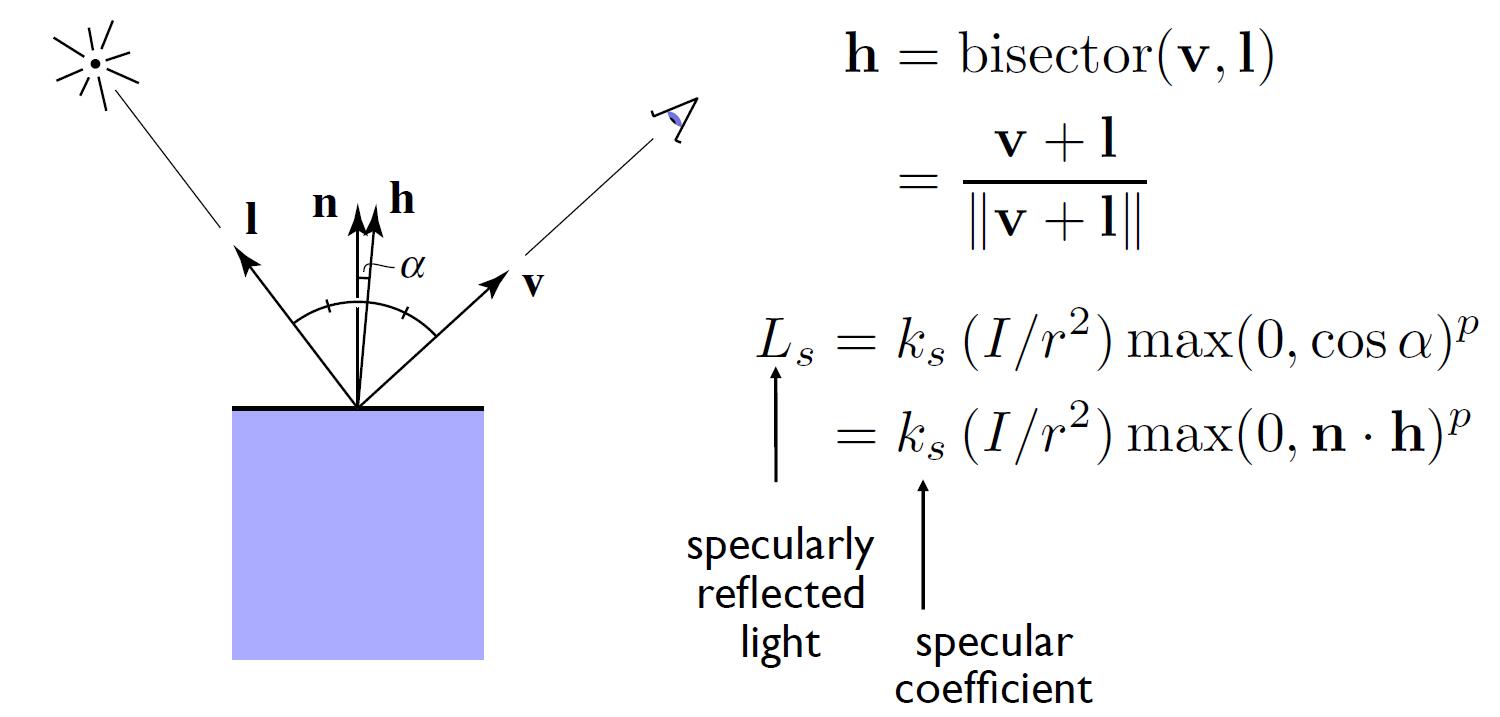
-
Specular coefficient: similar to diffuse coefficient, to describe the property and material of the object, but specular coefficient always set to 1, which means the shading point emmits white color when the specular reflection happens.
-
phong exponent: increasing phong exponent $p$ will narrow the reflection lobe and accelerate the decay rate of the specular reflection effect as the angle increased.
- When the angle between the reflected light and view direction more than 3~5 degree, we suppose specular reflection disappears.
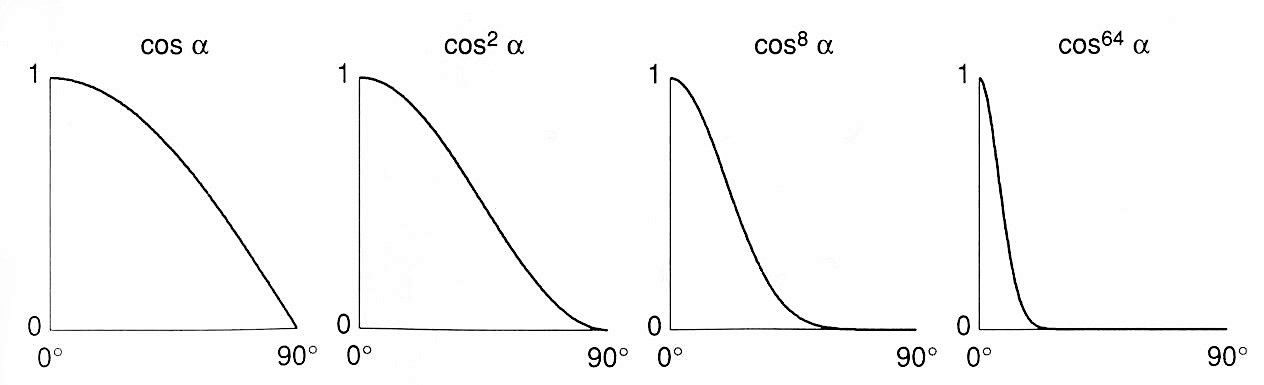

Tip: Compared to diffuse reflection, we ignore the energy received term for simplicity. Note that Blinn-Phong model is just an empirical model.
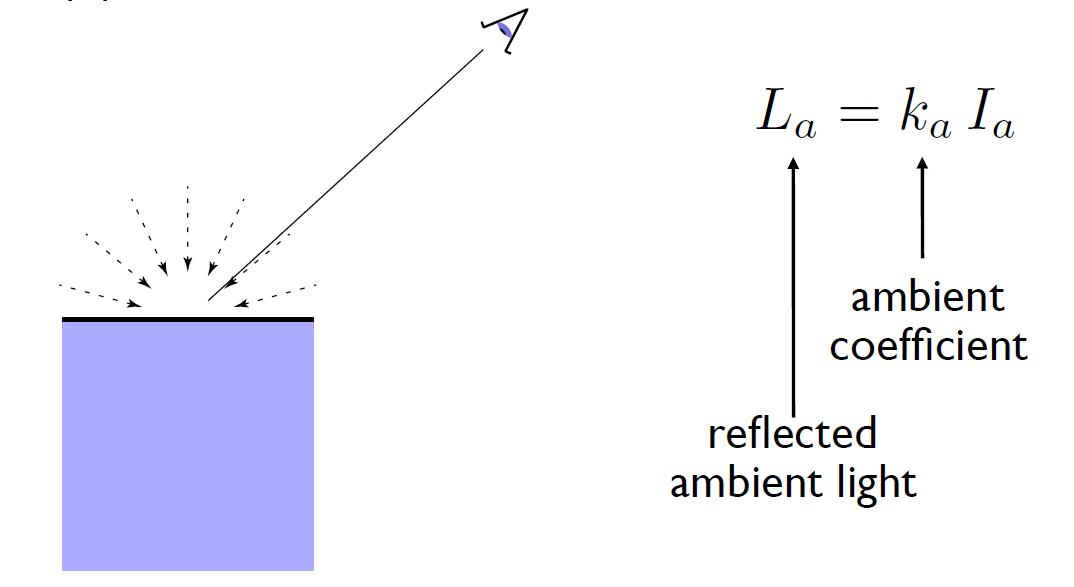
Ambient Term
- Shading that does not depend on anything
- Independent of light $l$ and view direction $v$
- Add constant color to account for disregarded illumination and fill in black shadows
- This is approximate / fake!
- Ambient coefficient: similar to specular coefficient and diffuse coefficient, but this is always a constant.
Blinn-Phong Model

Shading Frequencies
- Flat (Face) shading (逐片元)
- Gouraud (Vertex) shading (逐顶点)
- Phong (Pixel) shading (逐像素)
Flat shading
- Shading for each triangle
normal vectorof each face is caluculated by cross product of triangle’s two edges- Not good for smooth surfaces

Gouraud shading
- Shading for each vertices and interpolate triangle from vertices
- Each vertex has a normal vector

- It is easy to obtain vertex normal from the underlying known geometry. e.g. sphere
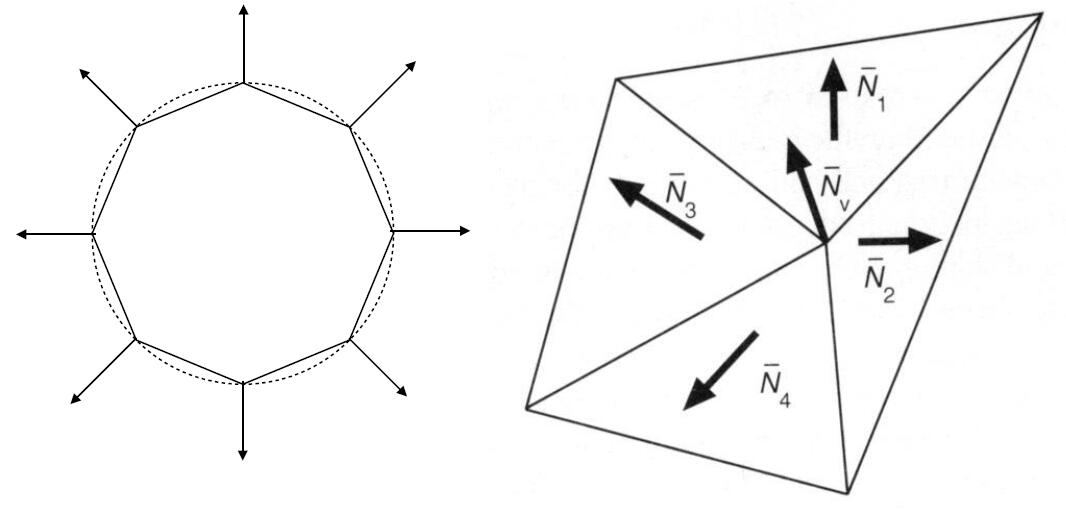
- Otherwise vertex normal can be inferred from surrounding triangle:
- average surrounding face normals
- weighted average surrounding face normals according to the area of each triangle
Phong shading
- Shading for each pixels across triangle
normal vectorof each pixels is interpolated by vertex vector

Tip: Phong shading is distinct from Blinn-Phong reflectance model
- pixel vector is computed by Barycentric interpolation of vertex normal
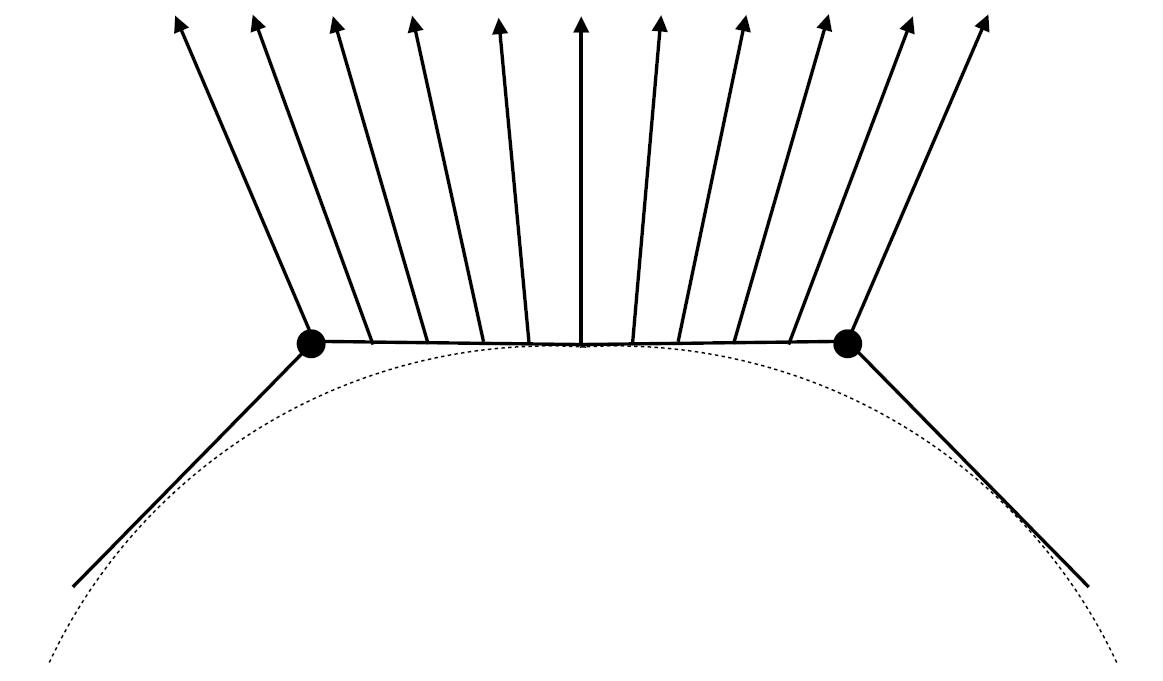
Caveat: remember to normalize each normal vector after each step of interpolation.
Shading difference
- As the model becomes more complex and has more vertices, the difference between three shading models become smaller

Shadow Mapping
- Draw shadows using rasterization
-
Shadow gives people the feeling of objects in contact with each other
- An Image-space Algorithm
- no knowledge of scene’s geometry required during shadow computation
- must deal with aliasing artifaces
- Key idea: the points NOT in shadow must be seen both by the light and by the camera
Note: Suppose the point light is the only source of light, which means the shadow of the object is 0 or 1, that is so-called hard shadow.
- Step 1: Assume the camera is at the point light source, perform depth test to record the depth information on the buffer.
- Step 2: From the view of the real camera, project all point in the view back to the point source light. If the the distance from the point to the light matches the depth, the point is visible, otherwise the point is blocked by other objects.
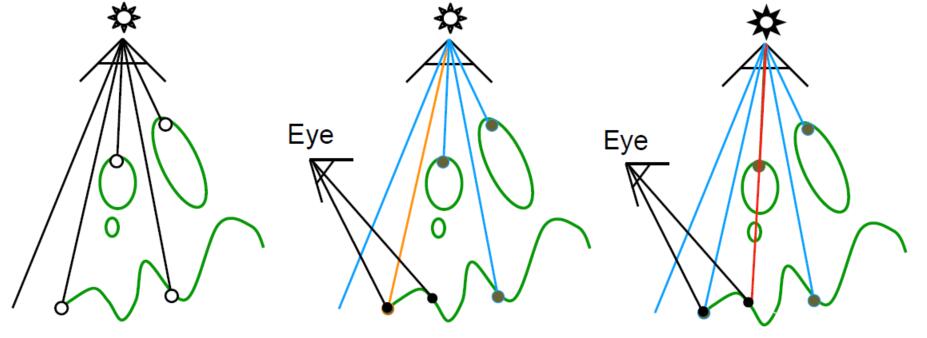
Visualizing Shadow Mapping
- A complex scene with shadows and without shadows
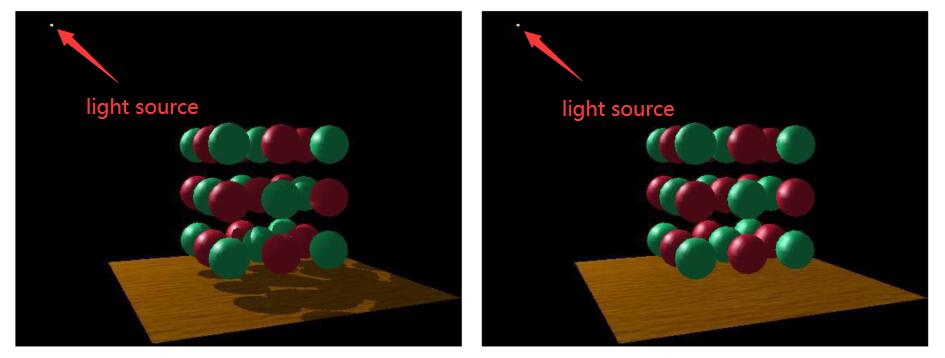
- The depth buffer from the light’s point of view
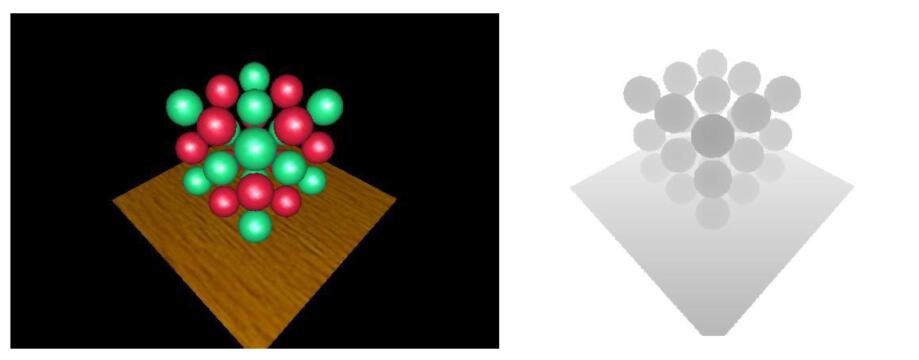
- The shadow from the camera’s point of view
- Green is where the distance from the light to shading point approximates to depth on buffer
- Non-green is where shadows should be
- Quality of shadow mapping is pretty bad due to the error caused by equality comparison of floating value

Problems with Shadow Mapping
- Only hard shadows in point light source can be mapped
- If the light source is not limited to one and no more point-like, the shadow will be not hard.
- Quality greatly depends on shadow map resolution, which is general problem with image-based rasterization techniques
Info: In many games settings, the shadow quality refers to the resolution of shadow map. The higher shadow quality sets, the better and more realistic the shadow will be mapped, and the higher it will cost.
- Errors involves equality comparison of floating point
- Sometimes use
biasorepsto approximate the equality between distance and depth in buffer
- Sometimes use
Hard vs. Soft Shadow
- Soft shadow is caused by the size of light source.
- The light is not able to reach anywhere in Umbra region.
- Part of light is blocked but still some light can illuminate Penumbra region.
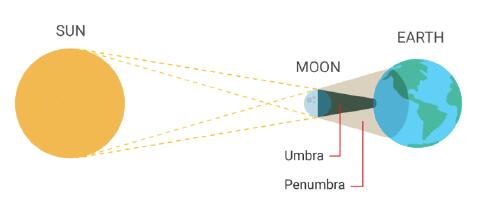
- Soft shadow is the transition from the umbra to penumbra to the illuminated region.
- The shadow corresponding to the edge of the object is gradually vague and soft due to the light illumination.
- Soft shadow is more realistic and natural because light source is not always point-like.

Graphics Pipeline
Real-time Rendering pipeline
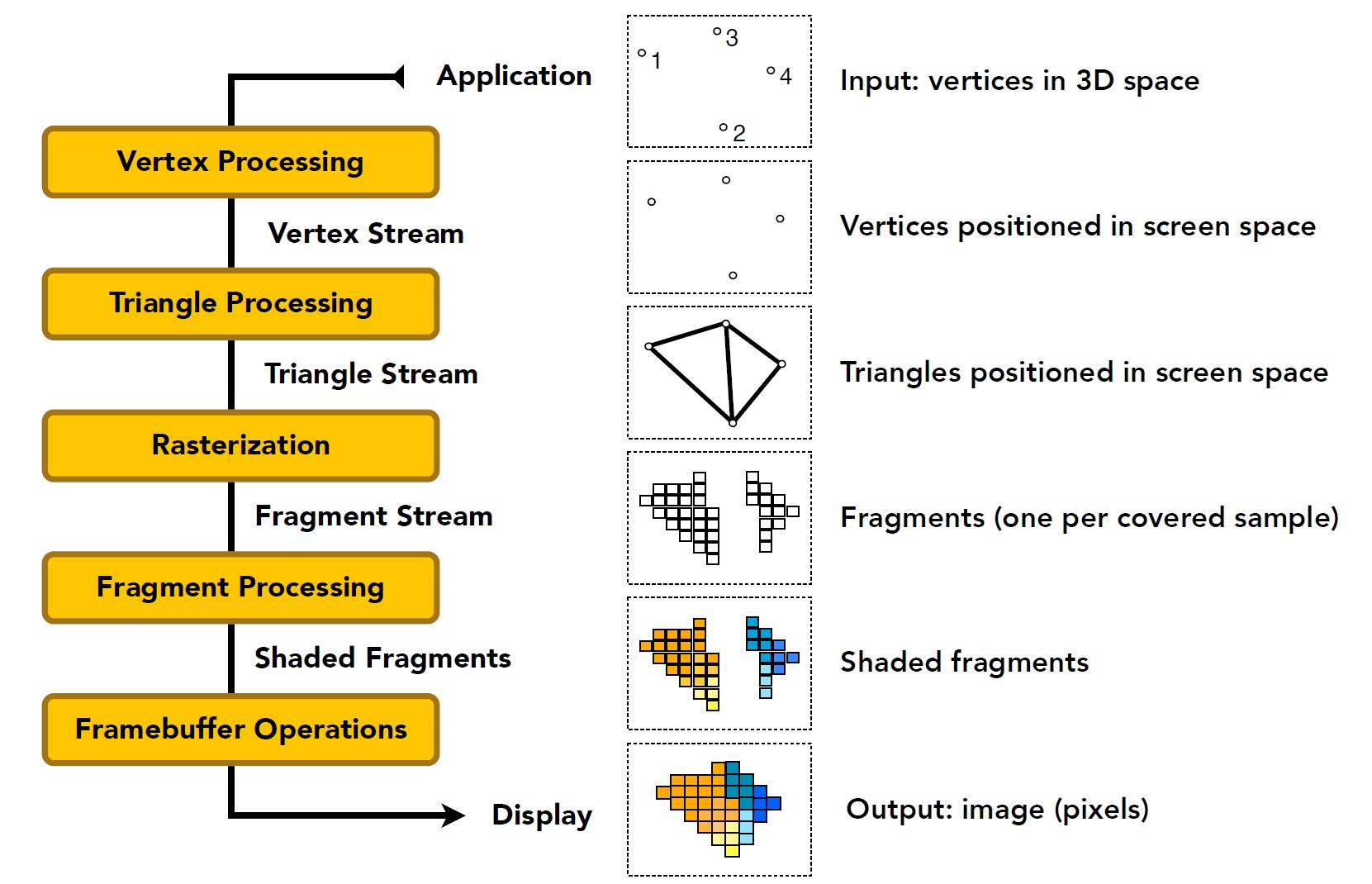
-
According to different shading frequency (face, vertex, pixel), Shading happens in Vertex Processing or Fragment Processing.
-
Texture mapping also happens in Vertex Processing and Fragment Processing.
-
Texture mapping is to assign vertices with different colors (properties, materials). This is the reason why objects look different in color and material after rendering. Detail in Texture later.
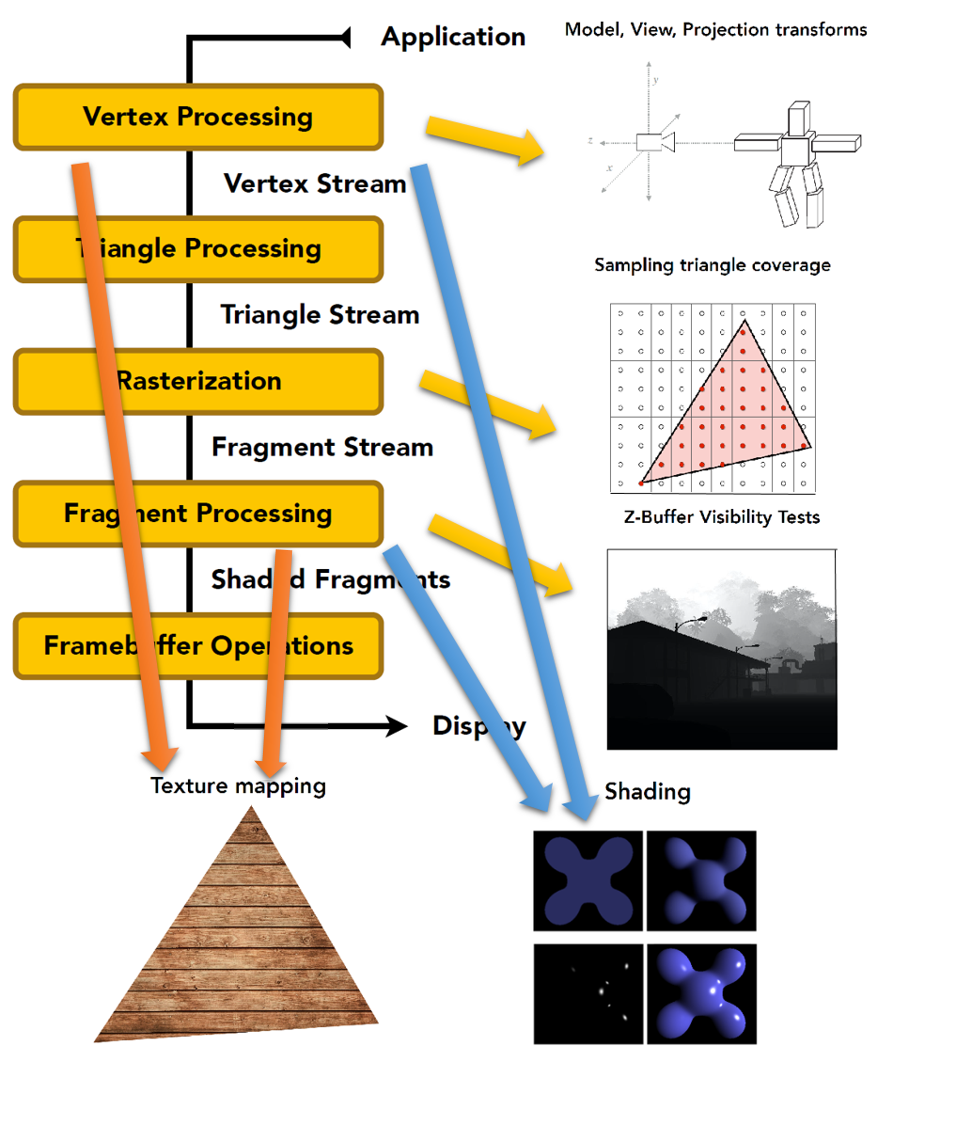
Note: Fragment (片元) is widely used in OpenGL and other modern API, which commonly means Pixel. Fragment shading (processing) = Pixel shading (processing).
Shader Programs
- Modern GPU allows to custom various shader by writing shader program
- Program vertex and fragment processing stages
- Describe operation on a single vertex or fragment. Shader function executes once per fragment, thus there is no need to loop or traverse each vertex or fragment
- Outputs color of surface at the current fragment’s screen sample position
// Example GLSL fragment shader program
uniform sampler2D myTexture; // texture property
uniform vec3 lightDir; // inversed light direction vector
varying vec2 uv; // perfragment value (interp. by rasterizer)
varying vec3 norm; // norm vector, perfragment value (interp. by rasterizer)
void diffuseShader() {
vec3 kd; // vector3d to store color value
kd = texture2d(myTexture, uv); // material color and property from texture
kd *= clamp(dot(–lightDir, norm), 0.0, 1.0); // diffuse shading
gl_FragColor = vec4(kd, 1.0); // assign fragment color value to gl_FragColor
}
- This shader performs a texture lookup to obtain the surface’s material color at this point
- Then performs a diffuse lighting calculation
- Vertex shader (顶点着色器) programs to each vertex, fragment shader (片元/像素着色器) programs to each pixel
Info: Incredible shader program and website: shadertoy.com
Highly Complex 3D Scenes in Realtime
- Modern GPU could handle much complex 3D scenes in realtime by deploying great amount of computation in parallel.
- thousands to millions of triangles in a scene
- Complex vertex and fragment shader computations
- High resolution (2-4 megapixel and supersampling)
- 30-60 fps (frames per second) and even higher for VR
- Game engine (architecture) is designed for developers to focus more on constructing games instead of techniques of graphics or rendering. The core functionality typically by a game engine includes a rendering engine (renderer) for 2D or 3D graphics (including shadows, global illumination etc.), a physics engine including collision detection and response, animation, artifical intelligence, sounding, memory management, threading, precomputation etc.
GPU: Graphics Pipeline Implementation
- Specialized processors for executing graphics pipeline computations
- Heterogeneous, Multi-core Processor
- Emerge different new shaders:
- Geometry shader: govern the processing of primitives and produce more triangles
- Compute shader: more general purpose for different computing
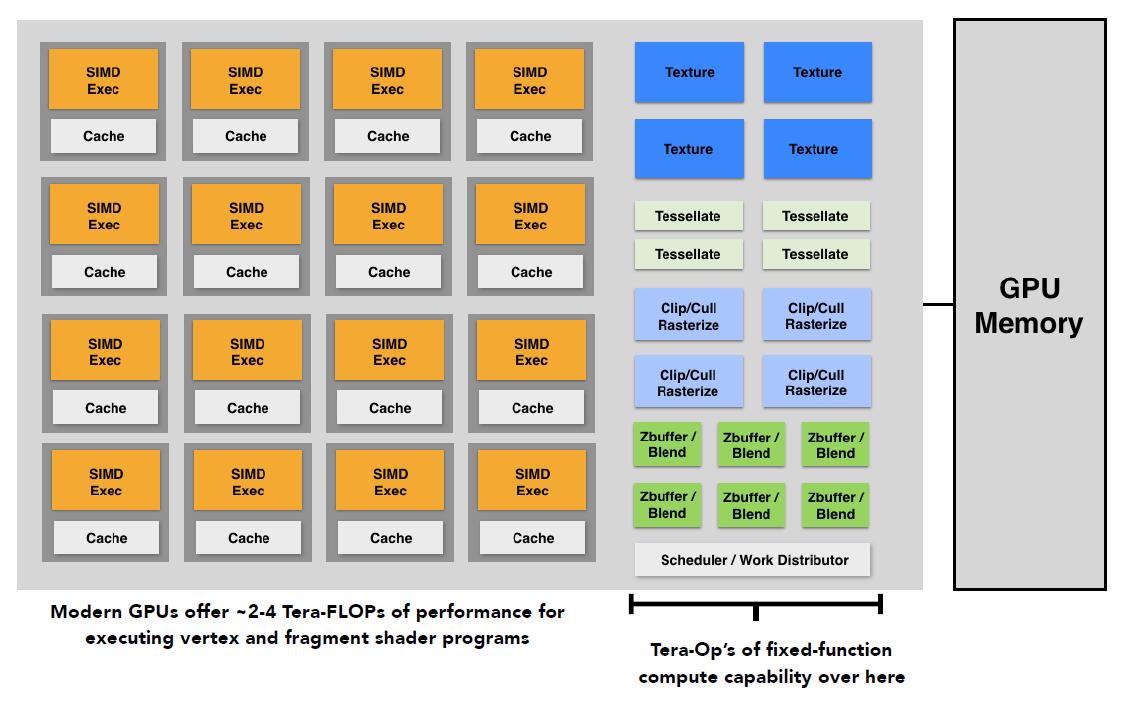
- FLOPS (floating point operatins per second): measure of computer performance:
| Prefix | Abbreviation | Order of magnitude | Computer performance | Storage capacity |
|---|---|---|---|---|
| mega- | M | $10^6$ | megaFLOPS (MFLOPS) | megabyte (MB) |
| giga- | G | $10^9$ | gigaFLOPS (GFLOPS) | gigabyte (GB) |
| tera- | T | $10^{12}$ | teraFLOPS (TFLOPS) | terabyte (TB) |
| peta- | P | $10^{15}$ | petaFLOPS (PFLOPS) | petabyte (PB) |
| exa- | E | $10^{18}$ | exaFLOPS (EFLOPS) | exabyte (EB) |
| zetta- | Z | $10^{21}$ | zettaFLOPS (ZFLOPS) | zettabyte (ZB) |
| yotta- | Y | $10^{24}$ | yottaFLOPS (YFLOPS) | yottabyte (YB) |